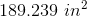There are six faces to a right, rectangular prism. Based on our dimensions, we know that we must have a face that is 12.4 x 2.3, a face that is 2.3 x 33 and a face that is 33 x 12.4. To think this through, imagine that the front face is 12.4 x 2.3, the left side is 2.3 x 33, and the top is 33 x 12.4. Now, each of these sides has a matching side opposite (the left has the right, the top has the bottom, the front has the back).

Therefore, we know we have the following areas for the faces of our prism:

2 * 12.4 * 2.3 = 57.04

2 * 2.3 * 33 = 151.8

2 * 12.4 * 33 = 818.4

Add these to get the total surface area:

57.04 + 151.8 + 818.4 = 1027.24

Based on our prompt, we can say that the prism has dimensions that can be represented as:

Dim1: x

Dim2: 2 * Dim1 = 2x

Dim3: 2 * Dim2 = 2 * 2x = 4x

More directly stated, therefore, our dimensions are: x, 2x, and 4x. Therefore, the volume is x * 2x * 4x = 216, which simplifies to 8x³ = 216 or x³ = 27. Solving for x, we find x = 3. Therefore, our dimensions are:

x = 3

2x = 6

4x = 12

Or: 3 x 6 x 12

Now, to find the surface area, we must consider that this means that our prism has sides of the following dimensions: 3 x 6, 6 x 12, and 3 x 12. Since each side has a "matching" side opposite it, we know that we have the following values for the areas of the faces:

2 * 3 * 6 = 36

2 * 6 * 12 = 144

2 * 3 * 12 = 72

The total surface area therefore equals: 36 + 144 + 72 = 252 square units.

Converting squared units is not difficult, though you have to be careful not to make a simple mistake. It is tempting to think you can merely divide the initial value (30,096) by 12, as though you were converting from inches to feet.

Begin by thinking this through as follows. In the case of a single dimension, we know that:

1 ft = 12 in   or   1 in = (1/12) ft

Now, think the case of a square with dimensions 1 ft x 1 ft. This square has the following dimensions in inches: 12 in x 12 in. The area is therefore 12 * 12 = 144 in². This holds for all two-dimensional conversions. Therefore, the two dimensional conversion equation is:

1 ft² = 144 in²   or   1 in² = (1/144) ft²

Based on this, we can convert our value 30,096 in² thus: 30,096/144 = 209 ft².

Converting squared units is not difficult, though you have to be careful not to make a simple mistake. It is tempting to think you can merely multiply the initial value (24) by 36, as though you were converting from yards to inches.

Begin by thinking this through as follows. In the case of a single dimension, we know that:

1 yd = 36 in

Now, think the case of a square with dimensions 1 yd x 1 yd. This square has the following dimensions in inches: 36 in x 36 in. The area is therefore 36 * 36 = 1296 in². This holds for all two-dimensional conversions. Therefore, the two dimensional conversion equation is:

1 yd² = 1296 in²

Based on this, we can convert our value 24 yd² thus: 24 * 1296 = 31,104 in².

First we must calculate the surface area of the cube. We know that there are six surfaces and each surface has the same area:

Now we will determine the amount of paint needed

The surface area of the prism can be broken into three rectangular sides and two equilateral triangular bases.

The area of the sides is given by:  , so for all three sides we get .

The equilateral triangle is also an equiangular triangle by definition, so the base has congruent sides of 6 in and three angles of 60 degrees.  We use a special right traingle to figure out the height of the triangle: 30 - 60 - 90.  The height is the side opposite the 60 degree angle, so it becomes or 5.196. 

The area for a triangle is given by  and since we need two of them we get .

Therefore the total surface area is .

The surface area of a rectangular prism is . Our prism, however, is missing its top, so it will be . This gives us .

Volume of a pyramid is

Thus:

Area of the base is .

Therefore, each side is .

If the height, which is twice the length of the base edges, measures 6 meters, then each base edge must measure 3 meters.  

Since the base is a square, the area of the base is 3 x 3 = 9.  

Therefore the volume of the right pyramid is V = (1/3) x area of the base x height = 1/3(9)(6) = 18.

If one edge of the base is 2.7 inches, and the height of the pyramid is equal to the diagonal of the base, we can find the height using the edge. The height is going to be equal to . The area of the base is . Volume of a pyramid is equal to  

This leaves us with