All PSAT Math Resources
Example Questions
Example Question #551 : Grade 8
Matt conducted a statistical experiment to determine the relationship between yearly salary earned and age. In this study, he assigned age (in years) as the independent variable, and yearly salary as the dependent variable. He plotted his results on a scatter plot. If the results follow a linear relationship, what is a reasonable conclusion that could be found based these results?
An undefined slope
A positive slope
A slope of
A negative slope
A positive slope
To help us answer this question, let's think about what we know about jobs:
If you were to get a part time job when you turn 

Example Question #1 : Drawing Conclusions From Graphs & Tables
A school principal conducted a statistical experiment to determine the relationship between 

A negative slope
A slope of
An undefined slope
A positive slope
A positive slope
We know, from attending school ourselves, that completing homework assignments and studying for quizzes and tests means that we will do better in school than if we didn't do those things. Completing homework and studying for tests takes time outside of school. Normally, the harder you study and the more time you spend studying, the more likely you are to do well in school. If you don't study at all, nor spend anytime completing homework assignments, your school grade will likely be lower than if you had spent time preparing and completing assignments; thus, we can conclude that the more time we spend studying, the higher our 

Example Question #1 : Use The Equation Of A Linear Model To Solve Problems: Ccss.Math.Content.8.Sp.A.3
Mrs. Frame conducted a statistical experiment to determine the relationship between test grades and the number of hours her students spent studying. In this study, she assigned the number of hours spent studying as the independent variable, and the test grades (in percentages) were assigned as the dependent variable. She plotted her results on a scatter plot. If the results follow a linear relationship, what is a reasonable conclusion that could be found based these results?
An undefined slope
A positive slope
A slope of
A negative slope
A positive slope
We know, from attending school ourselves, that when we have a test coming up that we want to do well on, we'll study for the test. Normally, the harder you study and the more time you spend studying, the more likely you are to do well on the test. If you don't study at all, and don't know the material that's being covered on a test, you'll like do poorly on a test; thus, we can conclude that the more time we spend studying, the higher our test grade will be. As the number of hours studied increases, the score on the test will increase; thus, the best fit line will have a positive slope.
Example Question #1 : Drawing Conclusions From Graphs & Tables
A doctor conducted a statistical experiment to determine the relationship between age and height. In this study, she assigned age as the independent variable, and height (in inches) as the dependent variable. She plotted the data on a scatter plot. The doctor drew a line of best fit and found the 

The average person has a height of
Every month a person grows by
Every year a person grows by
A newborn baby will have an average height of
A newborn baby will have an average height of
The question tells us that age is the independent variable, or the 
The 


Example Question #2171 : Psat Mathematics
A used car dealership conducted a statistical experiment to determine the relationship between the age of a car and the cost. In this study, he assigned age as the independent variable, and price as the dependent variable. He plotted the data on a scatter plot and drew a line of best fit. The 

As a car ages, the price increases by
The slope for the best fit line of this data set is
The price of a brand new car is
AS a car ages, the price decreases by
The price of a brand new car is
The question tells us that age is the independent variable, or the 
The 


Example Question #2 : Use The Equation Of A Linear Model To Solve Problems: Ccss.Math.Content.8.Sp.A.3
A used car dealership conducted a statistical experiment to determine the relationship between the age of a car and the cost. In this study, he assigned age as the independent variable, and price as the dependent variable. He plotted the data on a scatter plot and drew a line of best fit. If the results follow a linear relationship, what is a reasonable conclusion that could be found based these results?
An undefined slope
A slope of
A positive slope
A negative slope
A negative slope
Imagine that you were buying a car. You have two options: a brand new car for 

Example Question #2 : Use The Equation Of A Linear Model To Solve Problems: Ccss.Math.Content.8.Sp.A.3
A doctor conducted a statistical experiment to determine the relationship between weight and height. In this study, she assigned weight as the independent variable, and height (in inches) as the dependent variable. She plotted the data on a scatter plot. If the results follow a linear relationship, what is a reasonable conclusion that could be found based these results?
An undefined slope
A positive slope
A negative slope
A slope of
A positive slope
Let's think about ourselves in this scenario, as you've gotten taller, has your weight increased or decreased? Most likely, as your height has increased your weight has also increased; thus the slope of the best fit line for this data would be positive.
Example Question #11 : Use The Equation Of A Linear Model To Solve Problems: Ccss.Math.Content.8.Sp.A.3
A school principal conducted a statistical experiment to determine the relationship between 



A student who studied 

Every 
The average student 
Every week of studying increased a student's 
A student who studied 

The question tells us that the hours spent per week studying is the independent variable, or the 

The 


Example Question #1 : Use The Equation Of A Linear Model To Solve Problems: Ccss.Math.Content.8.Sp.A.3
Mr. Miller conducted a statistical experiment to determine the relationship between final grades and the number of school days that his students missed. In this study, he assigned the number of missed school days as the independent variable, and the final grade was assigned as the dependent variable. Every student started the class with a 

The equation of the best fit line will be in slope intercept form:
The question tells us that days are the independent variable, or 
Every students starts with a 




The final piece that we need is the slope, or 

If we put all of the pieces together, then the equation for the line of best fit is the following:
Example Question #1 : Use Data To Construct And Interpret A Two Way Table: Ccss.Math.Content.8.Sp.A.4
A teacher at a high school conducted a survey of seniors and found that 



To help answer this question, we can construct a two-way table and fill in our known quantities from the question.
The columns of the table will represent the students who have a laptop or do not have a laptop and the rows will contain the students who have a car or do not have a car. The first bit of information that we were given from the question was that 








Our question asked how many students have a laptop, but do not own have a car. We can take the total number of students that own a lap top, 
This means that 
Certified Tutor
All PSAT Math Resources








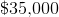
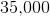




















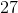


![\frac{\begin{array}[b]{r}81\\ -\ 54\end{array}}{ \ \ \ \space 27}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/980467/gif.latex)



