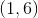We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Graphing

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #14 : Graphing Lines

A line graphed on the coordinate plane below. Graph_of_y_-2x_4

Give the equation of the line in slope intercept form.

Possible Answers:

$\dpi{100} \small y=2x+4$

$\dpi{100} \small y=-x+4$

$\dpi{100} \small y=-2x+4$

$\dpi{100} \small y=-2x-4$

$\dpi{100} \small y=2x-4$

Correct answer:

$\dpi{100} \small y=-2x+4$

Explanation:

The slope of the line is $\dpi{100} \small -2$ and the y-intercept is $\dpi{100} \small 4$ .

The equation of the line is $\dpi{100} \small y=-2x+4$ .

Report an Error

Example Question #13 : Graphing

Graph_of_y_-x_3

Give the equation of the curve.

Possible Answers:

$\dpi{100} \small y=x^{3}$

$\dpi{100} \small y=-x^{3}$

$\dpi{100} \small y=-x^{2}$

None of the other answers

$\dpi{100} \small y=x^{4}$

Correct answer:

$\dpi{100} \small y=-x^{3}$

Explanation:

Graph_of_x_3 This is the parent graph of $\dpi{100} \small x^{3}$ . Since the graph in question is negative, then we flip the quadrants in which it will approach infinity. So the graph of $\dpi{100} \small y=-x^{3}$ will start in quadrant 2 and end in 4.

Report an Error

Example Question #671 : Sat Mathematics

The equation 3x + 2y = 6 represents a line. This line does NOT pass through which of the four quadrants?

Possible Answers:

III

Cannot be determined

Correct answer:

III

Explanation:

Plug in for to find a point on the line:

3(0) + 2y = 6

y = 3

Thus, (0,3) is a point on the line.

Plug in for to find a second point on the line:

3x + 2(0) = 6

x = 2

(2,0) is another point on the line.

Now we know that the line passes through the points (2,0) and (0,3) .

A quick sketch of the two points reveals that the line passes through all but the third quadrant.

Report an Error

Example Question #1 : Graphing

Psat1question

What is the equation of the line in the graph above?

Possible Answers:

y = 2x-1

y = 2x +1

y = x + 2

y=x-1

y = x + 1

Correct answer:

y = 2x-1

Explanation:

In order to find the equation of a line in slope-intercept form $\left( y = mx+b$ , where is the slope and is the y-intercept), one must know or otherwise figure out the slope of the line (its rate of change) and the point at which it intersects the y-axis. By looking at the graph, you can see that the line crosses the y-axis at y=-1 . Therefore, b=-1 .

Slope is the rate of change of a line, which can be calculated by figuring out the change in y divided by the change in x, using the formula

$m = \frac{\Delta y}{\Delta x} = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ .

When looking at a graph, you can pick two points on a graph and substitute their x- and y-values into that equation. On this graph, it's easier to choose points like (0,-1) and (1,1) . Plug them into the equation, and you get

$m = \frac{1+1}{1-0} = \frac{2}{1} = 2$

Plugging in those values for and in the equation, and you get y=2x-1

Report an Error

Example Question #2 : Graphing

What are the x- and y- intercepts of the equation y = 4x -2 ?

Possible Answers:

$\left ( 4,0\right )\ \textup{and}\ \left ( 0,-2\right )$

$\left ( -2,0\right )\ \textup{and}\ \left ( 0,\frac{1}{2}\right )$

$\left ( -2,0\right )\ \textup{and}\ \left ( 0,4\right )$

$\left ( -2,0\right )\ \textup{and}\left ( 0,-4\right )$

$\left ( \frac{1}{2},0 \right )\textup{and}\left ( 0,-2\right )$

Correct answer:

$\left ( \frac{1}{2},0 \right )\textup{and}\left ( 0,-2\right )$

Explanation:

Answer: (1/2,0) and (0,-2)

Finding the y-intercept: The y-intercept is the point at which the line crosses tye y-axis, meaning that x = 0 and the format of the ordered pair is (0,y) with y being the y-intercept. The equation y=4x-2 is in slope-intercept ( y=mx+b ) form, meaning that the y-intercept, b, is actually given in the equation. b = -2, which means that our y-intercept is -2. The ordered pair for expressing this is (0,-2)

Finding the x-intercept: To find the x-intercept of the equation y=4x-2 , we must find the point where the line of the equation crosses the x-axis. In other words, we must find the point on the line where y is equal to 0, as it is when crossing the x-axis. Therefore, substitute 0 into the equation and solve for x: 0=4x-2

2 = 4x

1/2=x

The x-interecept is therefore (1/2,0).

Report an Error

Example Question #3 : Graphing

Which of the following could be the equation of the line shown in this graph?

Line

Possible Answers:

$y=-\frac{2}{3}x +1$

$y=\frac{2}{3}x +2$

$y=-\frac{7}{6}x -4$

$y=\frac{4}{3}x -5$

$y=-\frac{5}{7}x -1$

Correct answer:

$y=-\frac{2}{3}x +1$

Explanation:

The line in the diagram has a negative slope and a positive y-intercept. It has a negative slope because the line moves from the upper left to the lower right, and it has a positive y-intercept because the line intercepts the y-axis above zero.

The only answer choice with a negative slope and a positive y-intercept is

$y=-\frac{2}{3}x +1$

Report an Error

Example Question #3 : Graphing

Which of the following coordinate pairs is farthest from the origin?

Possible Answers:

(-1, 8)

(0, 7)

(3, 4)

(1, 6)

(2, 5)

Correct answer:

(-1, 8)

Explanation:

Using the distance formula, calculate the distance from each of these points to the origin, (0, 0). While each answer choice has coordinates that add up to seven, (-1, 8) is the coordinate pair that produces the largest distance, namely $\sqrt{65}$ , or approximately 8.06.

Report an Error

Example Question #1 : How To Graph A Point

A point at $\left ( -3,6\right )$ in the standard coordinate plane is shifted right 5 units and down 3 units. What are the new coordinates of the point?

Possible Answers:

$\left ( 5,3\right )$

$\left ( -5,-3\right )$

$\left ( 2,3\right )$

$\left ( 0,0\right )$

$\left ( -6,-12\right )$

Correct answer:

$\left ( 2,3\right )$

Explanation:

The point $\left ( -3,6\right )$ shifted to the right 5 units will shift along the x-axis, meaning that you will add 5 to the original x-coordinate, so the new x=2 . The point shifted down by three units will shift down the y-axis, meaning that you will subtract three from the original y-coordinate, so the new y=3 .

The resultant coordinate is $\left ( 2,3\right )$ .

Report an Error

Example Question #2 : Graphing

Axes_1

Give the coordinates of the point plotted in the above set of coordinate axes.

Possible Answers:

(2,-6)

(6, 2)

(2,6)

None of the other responses is correct.

(6, -2)

Correct answer:

(2,6)

Explanation:

The point can be reached from the origin by moving 2 units right then 6 units up. This makes the first coordinate 2 and the second coordinate 6.

Report an Error

Example Question #1 : How To Graph A Function

Which of the following could be a value of $f(x)$ for $f(x)=-x^2 + 3$ ?

Possible Answers:

$5$

$7$

$6$

$3$

$4$

Correct answer:

$3$

Explanation:

The graph is a down-opening parabola with a maximum of $y=3$ . Therefore, there are no y values greater than this for this function.

Report an Error

View PSAT Mathematics Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View PSAT Mathematics Tutors

Dr. Derrick
Certified Tutor

Huston-Tillotson University, Bachelor of Science, Mathematics. Grand Canyon University, Master of Arts, Education.

View PSAT Mathematics Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Washington DC, SSAT Tutors in Dallas Fort Worth, Spanish Tutors in Boston, French Tutors in San Diego, Algebra Tutors in Atlanta, Chemistry Tutors in Washington DC, Reading Tutors in San Francisco-Bay Area, English Tutors in New York City, Calculus Tutors in Seattle, ACT Tutors in Denver

Popular Courses & Classes

SAT Courses & Classes in Denver, SSAT Courses & Classes in Denver, MCAT Courses & Classes in Atlanta, SAT Courses & Classes in Chicago, SSAT Courses & Classes in Miami, LSAT Courses & Classes in Denver, MCAT Courses & Classes in Houston, GMAT Courses & Classes in Miami, ISEE Courses & Classes in Miami, ACT Courses & Classes in Miami

Popular Test Prep

SSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Phoenix, ISEE Test Prep in Miami, ACT Test Prep in Miami, ISEE Test Prep in Denver, GMAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Philadelphia, ACT Test Prep in Houston, SAT Test Prep in Houston, SAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Graphing

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #14 : Graphing Lines

Example Question #13 : Graphing

Example Question #671 : Sat Mathematics

Example Question #1 : Graphing

Example Question #2 : Graphing

Example Question #3 : Graphing

Example Question #3 : Graphing

Example Question #1 : How To Graph A Point

Example Question #2 : Graphing

Example Question #1 : How To Graph A Function

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: