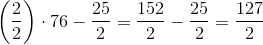PSAT Math : Fractions
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #31 : Fractions
In a classroom of 
To begin, you need to calculate how many students are taking Old Norse. This is:
Now, the ratio of students taking Old Norse to students taking Greek is the same thing as the fraction of students taking Old Norse to students taking Greek, or:
Next, just reduce this fraction to its lowest terms by dividing the numerator and denominator by their common factor of 
This is the same as 
Example Question #1 : How To Express A Fraction As A Ratio
In a garden, there are 
To begin, you need to do a simple addition to find the total number of flowers in the garden:
Now, the ratio of petunias to the total number of flowers in the garden can be represented by a simple division of the number of petunias by 
Next, reduce the fraction by dividing out the common 
This is the same as 
Example Question #1 : Complex Fractions
Simplify:
Simplify the numerator and the denominator, then divide, as follows:
Example Question #2 : Complex Fractions
Evaluate:
Simplify the numerator and the denominator, then divide, as follows:
Example Question #1 : How To Subtract Complex Fractions
Solve:
First reduce the fraction. We can divide both the numerator and the denominator by 3.
Now our expression looks like this:
When you add or subtract fractions, you need to have the same denominator. The lowest common deonminator here is 2. So we need to multiply and solve:
Example Question #113 : Fractions
Mr. Owens spent $7.50 for a dinner buffet. The amount he paid accounted for 3/4 of the money in his wallet. How much money is left in his wallet for other expenses?
$1.00
$10.00
$4.00
$2.50
$6.50
$2.50
If $7.50 is 3/4 of the total, 7.50/3 gives us what 1/4 of his total money would be. This equals $2.50, the remaining unspent quarter.
Example Question #1 : Whole And Part
A certain ball that is dropped will bounce back to 3/5 of the height it was initially dropped from. If after the 2nd bounce the ball reaches 39.96 ft, what was the initial height the ball was dropped from?
100 ft
66 ft
111 ft
135 ft
150 ft
111 ft
We know the height of the initial bounce, so work backwards to find the initial height. 39.96/0.6 = 66.6 = height of ball after first bounce
66.6/0.6 = 111 ft
Example Question #122 : Fractions
A pitcher of water is filled 
30
45
40
50
35
45
If 
Example Question #81 : Fractions
If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?
If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:
8 = (1/3) x, where x is the number in the entire class.
When we solve for x in the equation we get x = 24.
Example Question #3 : How To Find The Whole From The Part
A certain bakery makes chocolate, vanilla, red velvet, and carrot cupcakes in a ratio of 2:3:5:1. If that bakery makes 63 vanilla cupcakes in one day, what is the total number of cupcakes that the bakery made that day?
Because the bakery makes 63 vanilla cupcakes in one day, start by dividing the 63 by the vanilla part of the ratio, which is 3. 
Now add up the parts of your ratio: 
All PSAT Math Resources
