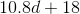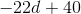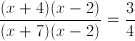Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Algebra

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Divide Polynomials

What is the remainder when the polynomial $x^{4} - 5x^{3} + 3x - 17$ is divided by x - 6 ?

Possible Answers:

2,411

215

217

2,341

Correct answer:

217

Explanation:

By the remainder theorem, if a polynomial p (x) is divided by the linear binomial x - c , the remainder is p(c) - that is, the polynomial evaluated at x = c . The remainder of dividing $x^{4} - 5x^{3} + 3x - 17$ by x - 6 is the dividend evaluated at x = 6 , which is

$x^{4} - 5x^{3} + 3x - 17$

$= 6^{4} - 5 \cdot 6^{3} + 3 \cdot 6 - 17$

$= 1,296 - 5 \cdot 216 + 18 - 17$

= 1,296 - 1,080 + 18 - 17

= 217

Report an Error

Example Question #1 : Multiplying And Dividing Polynomials

Simplify: $\frac{6x^7y^3z^9}{3x^6y^3z}$

Possible Answers:

xyz^8

xz^8

2xz^8

6xyz^8

xyz

Correct answer:

2xz^8

Explanation:

Cancel by subtracting the exponents of like terms:

$\frac{6x^7y^3z^9}{3x^6y^3z} = 2x^{7-6}y^{3-3}z^{9-1}=2xy^0z^8=2xz^8$

Report an Error

Example Question #1 : Binomials

Decrease 18d +30 by 40%. Which of the following will this be equal to?

Possible Answers:

18d -10

10.8d + 18

-22d + 40

10.8d + 30

18d +18

Correct answer:

10.8d + 18

Explanation:

A number decreased by 40% is equivalent to 100% of the number minus 40% of the number. This is taking 60% of the number, or, equivalently, multiplying it by 0.6.

Therefore, 18d +30 decreased by 40% is 0.6 times this, or

$0.6 \left (18d +30 \right ) = 0.6 \cdot 18d + 0.6 \cdot 30 = 10.8d + 18$

Report an Error

Example Question #1 : Binomials

Find the product:

(7-2y)(5-6y)

Possible Answers:

12y^2-52y+35

12y^2-32y+35

52y+35

12y^2-35

12y^2-52y

Correct answer:

12y^2-52y+35

Explanation:

Find the product:

(7-2y)(5-6y)

Use the distributive property:

7(5-6y)-2y(5-6y)

35-42y-10y+12y^2

Write the resulting expression in standard form:

12y^2-52y+35

Report an Error

Example Question #21 : Polynomials

If 〖(x+y)〗²= 144 and 〖(x-y)〗²= 64, what is the value of xy?

Possible Answers:

Correct answer:

Explanation:

We first expand each binomial to get x² + 2xy + y² = 144 and x² - 2xy + y² = 64. We then subtract the second equation from the first to find 4xy = 80. Finally, we divide each side by 4 to find xy = 20.

Report an Error

Example Question #1 : How To Simplify Binomials

Which of these expressions can be simplified further by collecting like terms?

Possible Answers:

None of the expressions in the other choices can be simplified further

$7ab+12ab^{2}$

$7b+13b^{2}$

12a+12b

7ab+13b

Correct answer:

None of the expressions in the other choices can be simplified further

Explanation:

A binomial can be simplified further if and only if the two terms have the same combination of variables and the same exponents for each like variable. This is not the case in any of the four binomials given, so none of the expressions can be simplified further.

Report an Error

Example Question #1 : Binomial Denominators

Solve for .

$\frac{x^{2}+2x-8}{x^{2}+5x-14}=\frac{3}{4}$

Possible Answers:

Correct answer:

Explanation:

$\frac{x^{2}+2x-8}{x^{2}+5x-14}=\frac{3}{4}$

Factor the expression

numerator: find two numbers that add to 2 and multiply to -8 [use 4,-2]

denominator: find two numbers that add to 5 and multiply to -14 [use 7,-2]

new expression:

$\frac{(x+4)(x-2)}{(x+7)(x-2)}=\frac{3}{4}$

Cancel the 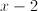x-2 and cross multiply.

4(x+4)=3(x+7)

4x+16=3x+21

x=5

Report an Error

Example Question #4522 : Algebra 1

Give the coefficient of $x^{2}$ in the product

$\left ( 2x + \frac{1}{3}\right ) \left ( x- \frac{1}{6}\right ) \left ( x+ \frac{1}{4}\right )$

Possible Answers:

$\frac{1}{6}$

$\frac{11}{12}$

$\frac{7}{6}$

$\frac{1}{4}$

$\frac{1}{2}$

Correct answer:

$\frac{1}{2}$

Explanation:

While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two terms and one constant are multiplied; find the three products and add them, as follows:

$\left ( \underline{2x }+ \frac{1}{3}\right ) \left ( \underline{x}- \frac{1}{6}\right ) \left ( x\underline{+ \frac{1}{4}}\right )$

$2x \cdot x \cdot \frac{1}{4} = \frac{1}{2}x^{2}$

$\left ( \underline{2x }+ \frac{1}{3}\right ) \left ( x \underline{- \frac{1}{6}}\right ) \left ( \underline{x}+ \frac{1}{4}\right )$

$2x \cdot \left (- \frac{1}{6} \right ) \cdot x = - \frac{1}{3}x^{2}$

$\left ( 2x\underline{ + \frac{1}{3}}\right ) \left ( \underline{x}- \frac{1}{6}\right ) \left ( \underline{x}+ \frac{1}{4}\right )$

$\frac{1}{3} \cdot x \cdot x= \frac{1}{3}x^{2}$

Add: $\frac{1}{2}x^{2} +\left ( - \frac{1}{3}x^{2} \right ) + \frac{1}{3}x^{2} = \frac{1}{2}x^{2}$

The correct response is $\frac{1}{2}$ .

Report an Error

Example Question #2 : How To Find The Value Of The Coefficient

Give the coefficient of $x^{5}$ in the binomial expansion of $\left ( 2x+ 0.5\right )^{8}$ .

Possible Answers:

26,880

224

1,680

Correct answer:

224

Explanation:

If the expression $\left ( A x + B\right )^{n}$ is expanded, then by the binomial theorem, the $x^{k}$ term is

$C(n, k) \cdot\left ( Ax \right )^{k} \cdot B ^{n - k}$

$= C(n, k) \cdot A ^{k} \cdot B ^{n - k} \cdot x^{k}$

or, equivalently, the coefficient of $x^{k}$ is

$C(n, k) \cdot A ^{k} \cdot B ^{n - k}$

Therefore, the $x^{5}$ coefficient can be determined by setting

A = 2, B =0.5, k=5, n = 8 :

$C(8,5) \cdot 2^{5} \cdot 0.5 ^{8-5}$

$=C(8,5) \cdot 2^{5} \cdot 0.5 ^{3}$

$= 56\cdot 32 \cdot 0.125$

=224

Report an Error

Example Question #1 : How To Find The Value Of The Coefficient

Give the coefficient of $x^{4}$ in the binomial expansion of $\left (6x+ \frac{1}{6}\right )^{7}$ .

Possible Answers:

5,040

140

210

$\frac{35}{6}$

Correct answer:

210

Explanation:

If the expression $\left ( A x + B\right )^{n}$ is expanded, then by the binomial theorem, the $x^{k}$ term is

$C(n, k) \cdot\left ( Ax \right )^{k} \cdot B ^{n - k}$

$= C(n, k) \cdot A ^{k} \cdot B ^{n - k} \cdot x^{k}$

or, equivalently, the coefficient of $x^{k}$ is

$C(n, k) \cdot A ^{k} \cdot B ^{n - k}$

Therefore, the $x^{4}$ coefficient can be determined by setting

$A = 6, B = \frac{1}{6}, n = 7, k= 4$ :

$C(7,4) \cdot 6 ^{4} \cdot\left ( \frac{1}{6} \right ) ^{7-4}$

$=C(7,4) \cdot 6 ^{4} \cdot\left ( \frac{1}{6} \right ) ^{3}$

$=35 \cdot 1,296 \cdot \frac{1}{216}$

= 210

Report an Error

View PSAT Mathematics Tutors

Sumit
Certified Tutor

Calcutta University, Bachelor of Science, Mathematics. Indian Statistical Institute, Master of Science, Mathematics.

View PSAT Mathematics Tutors

Trenton
Certified Tutor

United States Military Academy, Bachelor of Science, Mathematics.

View PSAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Philadelphia, Computer Science Tutors in Atlanta, Chemistry Tutors in Houston, Math Tutors in Houston, MCAT Tutors in San Diego, Physics Tutors in Denver, Calculus Tutors in New York City, ACT Tutors in Phoenix, LSAT Tutors in Phoenix, GRE Tutors in Chicago

Popular Courses & Classes

ACT Courses & Classes in Seattle, MCAT Courses & Classes in San Diego, GRE Courses & Classes in San Diego, GRE Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Miami, GMAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Chicago, Spanish Courses & Classes in New York City, GRE Courses & Classes in Boston, ISEE Courses & Classes in Los Angeles

Popular Test Prep

GMAT Test Prep in Washington DC, LSAT Test Prep in New York City, LSAT Test Prep in Chicago, ISEE Test Prep in Washington DC, GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in Denver, SSAT Test Prep in Houston, GMAT Test Prep in San Diego, ACT Test Prep in Phoenix, SAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Algebra

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : How To Divide Polynomials

Example Question #1 : Multiplying And Dividing Polynomials

Example Question #1 : Binomials

Example Question #1 : Binomials

Example Question #21 : Polynomials

Example Question #1 : How To Simplify Binomials

Example Question #1 : Binomial Denominators

Example Question #4522 : Algebra 1

Example Question #2 : How To Find The Value Of The Coefficient

Example Question #1 : How To Find The Value Of The Coefficient

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: