All Precalculus Resources
Example Questions
Example Question #1331 : Pre Calculus
What is the amplitude of the following function?
24
14
-14
-24
24
When you think of a trigonometric function of the form y=Asin(Bx+C)+D, the amplitude is represented by A, or the coefficient in front of the sine function. While this number is -24, we always represent amplitude as a positive number, by taking the absolute value of it. Therefore, the amplitude of this function is 24.
Example Question #2 : Amplitude, Period, Phase Shift Of A Trig Function
Select the answer choice that correctly matches each function to its period.
The following matches the correct period with its corresponding trig function:
In other words, sin x, cos x, sec x, and csc x all repeat themselves every 

Example Question #3 : Amplitude, Period, Phase Shift Of A Trig Function
What is the period of this sine graph?

The graph has 3 waves between 0 and 


Example Question #2 : Amplitude, Period, Phase Shift Of A Trig Function
Write the equation for a cosine graph with a maximum at 

In order to write this equation, it is helpful to sketch a graph:
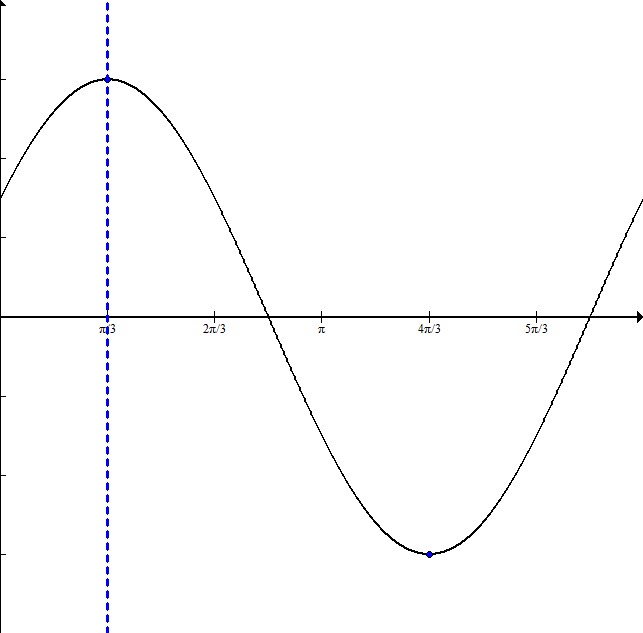
The dotted line is at 

The distance from the maximum to the minimum is half the entire wavelength. Here it is 
Since half the wavelength is 

The amplitude is 3 because the graph goes symmetrically from -3 to 3.
The equation will be in the form 
This equation is

Example Question #2 : Amplitude, Period, Phase Shift Of A Trig Function
Find the phase shift of 
-4
2
-2
3
-2
In the formula,


Plugging in what we know gives us:

Simplified, the phase is then 
Example Question #1 : Amplitude, Period, Phase Shift Of A Trig Function
Which equation would produce this sine graph?
The graph has an amplitude of 2 but has been shifted down 1:
In terms of the equation, this puts a 2 in front of sin, and -1 at the end.
This makes it easier to see that the graph starts [is at 0] where 
The phase shift is 

Example Question #7 : Amplitude, Period, Phase Shift Of A Trig Function
Which of the following equations could represent a cosine function with amplitude 3, period 

The form of the equation will be
First, think about all possible values of A that could give you an amplitude of 3. Either A = -3 or A = 3 could each produce amplitude = 3. Be sure to look for answer choices that satisfy either of these.
Secondly, we know that the period is 

Finally, we need to find a value of C that satisfies


Next, plug in B= 4 to solve for C:
Putting this all together, the equation could either be:

Example Question #8 : Amplitude, Period, Phase Shift Of A Trig Function
State the amplitude, period, phase shift, and vertical shift of the function
Amplitude: 7
Period: 
Phase Shift: 
Vertical Shift: -4
Amplitude: 7
Period: 
Phase Shift: -
Vertical Shift: -4
Amplitude: 7
Period: -
Phase Shift: -
Vertical Shift: -4
Amplitude: -7
Period: 
Phase Shift: -
Vertical Shift: 4
Amplitude: 7
Period: 
Phase Shift: -
Vertical Shift: -4
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
/|B|
- phase shift is -C/B
- vertical shift is D
In our equation, A=-7, B=6, C=
To find amplitude, look at the coefficient in front of the sine function. A=-7, so our amplitude is equal to 7.
The period is 2


To find the phase shift, take -C/B, or -
6x+
6x=-
x=-
Either way, our phase shift is equal to -
The vertical shift is equal to D, which is -4.
y=-7\sin(6x+\pi)-4
Example Question #9 : Amplitude, Period, Phase Shift Of A Trig Function
State the amplitude, period, phase shift, and vertical shift of the function
Amplitude: 1
Period:
Phase Shift:
Vertical Shift: 3
Amplitude: 1
Period:
Phase Shift:
Vertical Shift: 3
Amplitude: 1
Period:
Phase Shift:
Vertical Shift: 3
Amplitude: 1
Period:
Phase Shift:
Vertical Shift: 3
Amplitude: 1
Period:
Phase Shift:
Vertical Shift: 0
Amplitude: 1
Period:
Phase Shift:
Vertical Shift: 3
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
/|B|
- phase shift is -C/B
- vertical shift is D
In our equation, A=-1, B=1, C=-
To find amplitude, look at the coefficient in front of the sine function. A=-1, so our amplitude is equal to 1.
The period is 2

To find the phase shift, take -C/B, or 
x-
x=
Either way, our phase shift is equal to 
The vertical shift is equal to D, which is 3.
Example Question #10 : Amplitude, Period, Phase Shift Of A Trig Function
State the amplitude, period, phase shift, and vertical shift of the function
Amplitude: 1
Period:
Phase Shift: -3/2
Vertical Shift: 2
Amplitude: 1
Period:
Phase Shift: -3/2
Vertical Shift: -2
Amplitude: 1
Period:
Phase Shift: 3/2
Vertical Shift: 2
Amplitude: 1
Period: 3/2
Phase Shift:
Vertical Shift: 2
Amplitude: 1
Period:
Phase Shift: 3/2
Vertical Shift: 2
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
/|B|
- phase shift is -C/B
- vertical shift is D
In our equation, A=1, B=2, C=-3, and D=2. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.
To find amplitude, look at the coefficient in front of the sine function. A=1, so our amplitude is equal to 1.
The period is 2

To find the phase shift, take -C/B, or 3/2. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
2x-3=0
2x=3
x=3/2
Either way, our phase shift is equal to 3/2.
The vertical shift is equal to D, which is 2.
Certified Tutor
Certified Tutor
All Precalculus Resources

































































 /|B|
/|B|





















