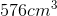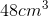We begin by recalling the volume of a pyramid.

$\displaystyle V=\frac{1}{3}Ah$ 

where $\displaystyle A$ is the area of the base and $\displaystyle h$ is the height.

Since the base is a square, we can find the area by squaring the length of one of the sides.

$\displaystyle A=4^2=16$

Given the height is 6cm, we can now calculate the volume.

$\displaystyle V=\frac{1}{3}(16)(6)=32$

Since all of the measurements were in centimeters, our volume will be in cubic centimeters. 

Therefore, the volume of Principal O'Shaughnessy's paperweight is $\displaystyle 32cm^3$.

The formula for the volume of a pyramid is $\displaystyle \frac{\left ( B \times h\right )}{3}$, where $\displaystyle B$ is the area of the base and $\displaystyle h$ is the height.

 Using this formula, 

$\displaystyle B$ = Area of the base, which is nothing but area of square with side $\displaystyle 9m$. $\displaystyle 9m \times 9m = 81 m^{2}$

Now, $\displaystyle \frac{81m^{2} \times h}{3} = 162 m^{3}$ when simplified, you get $\displaystyle 6m$.

Hence, the height of the pyramid is $\displaystyle 6m$.

Convert each measurement from inches to feet by multiplying it by 12:

Height: 4 feet = $\displaystyle 4 \times 12 = 48$ inches

Sidelength of the base: 3 feet = $\displaystyle 3 \times 12 = 36$ inches

The volume of a pyramid is 

$\displaystyle V = \frac{1}{3} Bh$

Since the base is a square, we can replace $\displaystyle B = s^{2}$:

$\displaystyle V = \frac{1}{3} s ^{2}h$

Substitute $\displaystyle s=36, h = 48$

$\displaystyle V = \frac{1}{3} \cdot 36 ^{2}\cdot 48$

$\displaystyle V =20,736$

The pyramid has volume 20,736 cubic inches.

Convert each of the measurements from feet to inches by multiplying by $\displaystyle 12$.

Height: $\displaystyle 2 \times 12 = 24$ inches

Sidelength of base: $\displaystyle 3 \times 12 = 36$ inches

The base of the pyramid has area 

$\displaystyle B = s^{2} = 36^{2} = 1,296$ square inches.

Substitute $\displaystyle B = 1,296, h = 24$  into the volume formula:

$\displaystyle V = \frac {1}{3} Bh$

$\displaystyle V = \frac {1}{3} \cdot 1,296 \cdot 24 =10,368$ cubic inches

The perimeter of the square base, $\displaystyle 3$ feet, is equivalent to $\displaystyle 3 \times 12 = 36$ inches; divide by $\displaystyle 4$ to get the sidelength of the base - and the height: $\displaystyle 36 \div 4 = 9$ inches. 

The area of the base is therefore $\displaystyle B = s^{2} = 9^{2} = 81$ square inches. 

In the formula for the volume of a pyramid, substitute $\displaystyle B = 81,h=9$:

$\displaystyle V = \frac{1}{3} Bh = \frac{1}{3}\cdot 81 \cdot 9 = 243$ cubic inches.

The volume of a pyramid can be determined using the following equation:

$\displaystyle V=\frac{1}{3}lwh=\frac{1}{3}(7)(6)(9)=126$

Write the formula for the volume of a pyramid.

$\displaystyle V=\frac{1}{3} (L\times W\times H)$

Substitute the dimensions and solve.

$\displaystyle V=\frac{1}{3} (2\times 4\times 6) = \frac{1}{3}(48)=16$

Write the volume formula for the pyramid.

$\displaystyle V=\frac{1}{3} (L\times W\times H)$

The base area is represented by $\displaystyle L\times W$.

Substitute the knowns into the formula.

$\displaystyle V=\frac{1}{3} (2\times 3) = \frac{1}{3} (6) =2$

Write the formula to find the area of a pyramid.

$\displaystyle V=\frac{1}{3} (L\times W \times H)$

Substitute the dimensions.

$\displaystyle V=\frac{1}{3} (4\times 7\times 3) = 28$

Write the formula for the volume of a pyramid.

$\displaystyle V=\frac{1}{3} (LWH)$

Substitute the dimensions and solve for the volume.

$\displaystyle V=\frac{1}{3} (10)(20)(40) = \frac{8000}{3}$