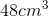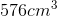Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Volume

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Volume

Principal O'Shaughnessy has a paperweight in the shape of a pyramid with a square base. If one side of the base has a length of 4cm and the height of the paperweight is 6cm, what is the volume of the paperweight?

Possible Answers:

32cm^3 $\displaystyle 32cm^3$

96cm^3 $\displaystyle 96cm^3$

576cm^3 $\displaystyle 576cm^3$

192cm^3 $\displaystyle 192cm^3$

48cm^3 $\displaystyle 48cm^3$

Correct answer:

32cm^3 $\displaystyle 32cm^3$

Explanation:

We begin by recalling the volume of a pyramid.

$V=\frac{1}{3}Ah$ $\displaystyle V=\frac{1}{3}Ah$

where $\displaystyle A$ is the area of the base and $\displaystyle h$ is the height.

Since the base is a square, we can find the area by squaring the length of one of the sides.

$\displaystyle A=4^2=16$

Given the height is 6cm, we can now calculate the volume.

$V=\frac{1}{3}(16)(6)=32$ $\displaystyle V=\frac{1}{3}(16)(6)=32$

Since all of the measurements were in centimeters, our volume will be in cubic centimeters.

Therefore, the volume of Principal O'Shaughnessy's paperweight is 32cm^3 $\displaystyle 32cm^3$.

Report an Error

Example Question #2 : Volume Of A Pyramid

The volume of a square pyramid is $162 m^{3}$ $\displaystyle 162 m^{3}$. If a side of the square base measures $\displaystyle 9m$. What is the height of the pyramid?

Possible Answers:

$\displaystyle 5m$

7.5m $\displaystyle 7.5m$

4.5m $\displaystyle 4.5m$

$\displaystyle 6m$

$\displaystyle 9m$

Correct answer:

$\displaystyle 6m$

Explanation:

The formula for the volume of a pyramid is $\frac{\left ( B \times h\right )}{3}$ $\displaystyle \frac{\left ( B \times h\right )}{3}$, where $\displaystyle B$ is the area of the base and $\displaystyle h$ is the height.

Using this formula,

$\displaystyle B$ = Area of the base, which is nothing but area of square with side $\displaystyle 9m$. $9m \times 9m = 81 m^{2}$ $\displaystyle 9m \times 9m = 81 m^{2}$

Now, $\frac{81m^{2} \times h}{3} = 162 m^{3}$ $\displaystyle \frac{81m^{2} \times h}{3} = 162 m^{3}$ when simplified, you get $\displaystyle 6m$.

Hence, the height of the pyramid is $\displaystyle 6m$.

Report an Error

Example Question #1 : Pyramids

A pyramid has height 4 feet. Its base is a square with sidelength 3 feet. Give its volume in cubic inches.

Possible Answers:

$5,184\textrm{ in}^{3}$ $\displaystyle 5,184\textrm{ in}^{3}$

$31,104\textrm{ in}^{3}$ $\displaystyle 31,104\textrm{ in}^{3}$

$124,416\textrm{ in}^{3}$ $\displaystyle 124,416\textrm{ in}^{3}$

$62,208 \textrm{ in}^{3}$ $\displaystyle 62,208 \textrm{ in}^{3}$

$20,736 \textrm{ in}^{3}$ $\displaystyle 20,736 \textrm{ in}^{3}$

Correct answer:

$20,736 \textrm{ in}^{3}$ $\displaystyle 20,736 \textrm{ in}^{3}$

Explanation:

Convert each measurement from inches to feet by multiplying it by 12:

Height: 4 feet = $4 \times 12 = 48$ $\displaystyle 4 \times 12 = 48$ inches

Sidelength of the base: 3 feet = $3 \times 12 = 36$ $\displaystyle 3 \times 12 = 36$ inches

The volume of a pyramid is

$V = \frac{1}{3} Bh$ $\displaystyle V = \frac{1}{3} Bh$

Since the base is a square, we can replace $B = s^{2}$ $\displaystyle B = s^{2}$:

$V = \frac{1}{3} s ^{2}h$ $\displaystyle V = \frac{1}{3} s ^{2}h$

Substitute $\displaystyle s=36, h = 48$

$V = \frac{1}{3} \cdot 36 ^{2}\cdot 48$ $\displaystyle V = \frac{1}{3} \cdot 36 ^{2}\cdot 48$

$\displaystyle V =20,736$

The pyramid has volume 20,736 cubic inches.

Report an Error

Example Question #3 : Pyramids

The height of a right pyramid is $\displaystyle 2$ feet. Its base is a square with sidelength $\displaystyle 3$ feet. Give its volume in cubic inches.

Possible Answers:

$15,552 \textrm{ in}^{3}$ $\displaystyle 15,552 \textrm{ in}^{3}$

$10,368 \textrm{ in}^{3}$ $\displaystyle 10,368 \textrm{ in}^{3}$

$41,472 \textrm{ in}^{3}$ $\displaystyle 41,472 \textrm{ in}^{3}$

$62,208\textrm{ in}^{3}$ $\displaystyle 62,208\textrm{ in}^{3}$

$31,104 \textrm{ in}^{3}$ $\displaystyle 31,104 \textrm{ in}^{3}$

Correct answer:

$10,368 \textrm{ in}^{3}$ $\displaystyle 10,368 \textrm{ in}^{3}$

Explanation:

Convert each of the measurements from feet to inches by multiplying by $\displaystyle 12$.

Height: $2 \times 12 = 24$ $\displaystyle 2 \times 12 = 24$ inches

Sidelength of base: $3 \times 12 = 36$ $\displaystyle 3 \times 12 = 36$ inches

The base of the pyramid has area

$B = s^{2} = 36^{2} = 1,296$ $\displaystyle B = s^{2} = 36^{2} = 1,296$ square inches.

Substitute $\displaystyle B = 1,296, h = 24$ into the volume formula:

$V = \frac {1}{3} Bh$ $\displaystyle V = \frac {1}{3} Bh$

$V = \frac {1}{3} \cdot 1,296 \cdot 24 =10,368$ $\displaystyle V = \frac {1}{3} \cdot 1,296 \cdot 24 =10,368$ cubic inches

Report an Error

Example Question #2 : Volume Of A Pyramid

The height of a right pyramid and the sidelength of its square base are equal. The perimeter of the base is 3 feet. Give its volume in cubic inches.

Possible Answers:

$81 \textrm{ in}^{3}$ $\displaystyle 81 \textrm{ in}^{3}$

$243 \textrm{ in}^{3}$ $\displaystyle 243 \textrm{ in}^{3}$

$729 \textrm{ in}^{3}$ $\displaystyle 729 \textrm{ in}^{3}$

$576 \textrm{ in}^{3}$ $\displaystyle 576 \textrm{ in}^{3}$

$27 \textrm{ in}^{3}$ $\displaystyle 27 \textrm{ in}^{3}$

Correct answer:

$243 \textrm{ in}^{3}$ $\displaystyle 243 \textrm{ in}^{3}$

Explanation:

The perimeter of the square base, $\displaystyle 3$ feet, is equivalent to $3 \times 12 = 36$ $\displaystyle 3 \times 12 = 36$ inches; divide by $\displaystyle 4$ to get the sidelength of the base - and the height: $36 \div 4 = 9$ $\displaystyle 36 \div 4 = 9$ inches.

The area of the base is therefore $B = s^{2} = 9^{2} = 81$ $\displaystyle B = s^{2} = 9^{2} = 81$ square inches.

In the formula for the volume of a pyramid, substitute $\displaystyle B = 81,h=9$:

$V = \frac{1}{3} Bh = \frac{1}{3}\cdot 81 \cdot 9 = 243$ $\displaystyle V = \frac{1}{3} Bh = \frac{1}{3}\cdot 81 \cdot 9 = 243$ cubic inches.

Report an Error

Example Question #3 : Solid Geometry

What is the volume of a pyramid with the following measurements?

$length=7; width=6;height=9;slant\ length=11$ $\displaystyle length=7; width=6;height=9;slant\ length=11$

Possible Answers:

126 $\displaystyle 126$

154 $\displaystyle 154$

462 $\displaystyle 462$

378 $\displaystyle 378$

Correct answer:

126 $\displaystyle 126$

Explanation:

The volume of a pyramid can be determined using the following equation:

$V=\frac{1}{3}lwh=\frac{1}{3}(7)(6)(9)=126$ $\displaystyle V=\frac{1}{3}lwh=\frac{1}{3}(7)(6)(9)=126$

Report an Error

Example Question #3 : Volume Of A Pyramid

The pyramid has a length, width, and height of 2,4,6 $\displaystyle 2,4,6$ respectively. What is the volume of the pyramid?

Possible Answers:

$\displaystyle 32$

$\displaystyle 48$

$\displaystyle 16$

$\displaystyle 26$

$\displaystyle 24$

Correct answer:

$\displaystyle 16$

Explanation:

Write the formula for the volume of a pyramid.

$V=\frac{1}{3} (L\times W\times H)$ $\displaystyle V=\frac{1}{3} (L\times W\times H)$

Substitute the dimensions and solve.

$V=\frac{1}{3} (2\times 4\times 6) = \frac{1}{3}(48)=16$ $\displaystyle V=\frac{1}{3} (2\times 4\times 6) = \frac{1}{3}(48)=16$

Report an Error

Example Question #2 : Volume

If the base area of the pyramid is $\displaystyle 2$, and the height is $\displaystyle 3$, what is the volume of the pyramid?

Possible Answers:

$\displaystyle 4$

$\displaystyle 9$

$\displaystyle 8$

$\displaystyle 6$

$\displaystyle 2$

Correct answer:

$\displaystyle 2$

Explanation:

Write the volume formula for the pyramid.

$V=\frac{1}{3} (L\times W\times H)$ $\displaystyle V=\frac{1}{3} (L\times W\times H)$

The base area is represented by $L\times W$ $\displaystyle L\times W$.

Substitute the knowns into the formula.

$V=\frac{1}{3} (2\times 3) = \frac{1}{3} (6) =2$ $\displaystyle V=\frac{1}{3} (2\times 3) = \frac{1}{3} (6) =2$

Report an Error

Example Question #3 : Volume

Find the volume of a pyramid with a length of 4, width of 7, and a height of 3.

Possible Answers:

$\displaystyle 48$

$\displaystyle 56$

$\displaystyle 96$

$\displaystyle 28$

$\displaystyle 84$

Correct answer:

$\displaystyle 28$

Explanation:

Write the formula to find the area of a pyramid.

$V=\frac{1}{3} (L\times W \times H)$ $\displaystyle V=\frac{1}{3} (L\times W \times H)$

Substitute the dimensions.

$V=\frac{1}{3} (4\times 7\times 3) = 28$ $\displaystyle V=\frac{1}{3} (4\times 7\times 3) = 28$

Report an Error

Example Question #4 : Volume Of A Pyramid

Find the volume of a pyramid if the length, base, and height are $\textup{10, 20, and 40,}$ $\displaystyle \textup{10, 20, and 40,}$ respectively.

Possible Answers:

$\frac{8000}{3}$ $\displaystyle \frac{8000}{3}$

$\frac{400}{3}$ $\displaystyle \frac{400}{3}$

500 $\displaystyle 500$

400 $\displaystyle 400$

$\frac{800}{3}$ $\displaystyle \frac{800}{3}$

Correct answer:

$\frac{8000}{3}$ $\displaystyle \frac{8000}{3}$

Explanation:

Write the formula for the volume of a pyramid.

$V=\frac{1}{3} (LWH)$ $\displaystyle V=\frac{1}{3} (LWH)$

Substitute the dimensions and solve for the volume.

$V=\frac{1}{3} (10)(20)(40) = \frac{8000}{3}$ $\displaystyle V=\frac{1}{3} (10)(20)(40) = \frac{8000}{3}$

Report an Error

View Pre-Algebra Tutors

Sreedhar
Certified Tutor

University of Oklahoma Norman Campus, Master of Engineering, Mechanical Engineering.

View Pre-Algebra Tutors

Cameron
Certified Tutor

Southern Illinois University-Systems Office, Bachelor of Science, Mechanical Engineering.

View Pre-Algebra Tutors

Kenneth
Certified Tutor

North Georgia University, Bachelors, Accounting. Brenau University, Masters, Business.

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Chicago, MCAT Tutors in Los Angeles, ISEE Tutors in New York City, Statistics Tutors in Washington DC, Chemistry Tutors in Chicago, GMAT Tutors in San Diego, French Tutors in Denver, English Tutors in Atlanta, Reading Tutors in Phoenix, Biology Tutors in Dallas Fort Worth

Popular Courses & Classes

MCAT Courses & Classes in Houston, Spanish Courses & Classes in Houston, Spanish Courses & Classes in Los Angeles, Spanish Courses & Classes in San Diego, ISEE Courses & Classes in Boston, SSAT Courses & Classes in Denver, LSAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Boston, Spanish Courses & Classes in Miami, SAT Courses & Classes in Philadelphia

Popular Test Prep

GRE Test Prep in Phoenix, GRE Test Prep in Chicago, GRE Test Prep in Philadelphia, MCAT Test Prep in Los Angeles, GMAT Test Prep in Denver, LSAT Test Prep in Los Angeles, LSAT Test Prep in Denver, GMAT Test Prep in Philadelphia, LSAT Test Prep in New York City, GRE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Volume

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #1 : Volume

Example Question #2 : Volume Of A Pyramid

Example Question #1 : Pyramids

Example Question #3 : Pyramids

Example Question #2 : Volume Of A Pyramid

Example Question #3 : Solid Geometry

Example Question #3 : Volume Of A Pyramid

Example Question #2 : Volume

Example Question #3 : Volume

Example Question #4 : Volume Of A Pyramid

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: