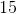This is a straightforward problem. Remember that when adding a negative number, you are actually subtracting:

Be sure to remember that the first number is also negative, meaning we are subtracting a number from a negative number:

The answer is -6.25.

The sum of two numbers of unlike sign is the difference of their absolute values, with the sign of the "dominant" number (the positive number here) affixed:

Subtract vertically by aligning the decimal points, making sure you append the 3.2 with a placeholder zero:

This is the correct choice.

To make  as small as possible, let  be as small as possible , and subtract the largest value of  possible :

To solve this problem, you need to get your variable isolated on one side of the equation:

Taking this step will elminate the  on the side with :

Now divide by  to solve for :

The important step here is to be able to add the negative numbers.  When you add negative numbers, they create lower negative numbers (if you prefer to think about it another way, you can think of adding negative numbers as subtracting one of the negative numbers from the other).  

Begin by isolating your variable.

Subtract  from both sides:

, or 

Next, subtract  from both sides:

, or 

Then, divide both sides by :

Recall that division of a negative by a negative gives you a positive, therefore:

 or 

To solve this equation, you need to isolate the variable on one side. We can accomplish this by dividing by  on both sides:

Anytime you divide, if the signs are the same (i.e. two positive, or two negative), you'll get a positive result.  If the signs are opposites (i.e. one positive, one negative) then you get a negative.  

Both of the numbers here are negative, so we will have a positive result:

To solve, you need to isolate the variable. We first subtract  then divide by :

When dividing, if the signs of the numbers are the same (i.e. both positive, or both negative), you yield a positive result.  If the signs of the numbers are opposites (i.e. one of each), then you yield a negative result.  

Therefore:

When two negative values are multiplied, the answer becomes positive. Then, we multiply normally. We should get  or .

Remember PEMDAS. The parentheses comes first. When adding a negative value, the operation is subtraction. We now have . The answer in the parentheses is , but since there is a negative sign outside, we need to add that in so final answer becomes . 

To determine the answer, it's best to compare the values without doing any math. Since  is bigger than  and the  has the positive sign in front, the answer is positive. Also, with addition, you can rewrite the expression without altering the answer. So, instead we can write . The positive and negative value combined gives us a negative sign and now we have  or .