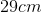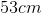All MCAT Physical Resources
Example Questions
Example Question #1 : Torque
A 2kg mass is suspended on a rope that wraps around a frictionless pulley attached to the ceiling with a mass of 0.01kg and a radius of 0.25m. The other end of the rope is attached to a massless suspended platform, upon which 0.5kg weights may be placed. While the system is initially at equilibrium, the rope is later cut above the weight, and the platform subsequently raised by pulling on the rope.

What is the torque on the pulley when the system is motionless?
0N*m
9.8N*m
10N*m
19.6N*m
0N*m
The net torque on the pulley is zero. Remember that 
In the image below, T1 (due to the platform with the 4 0.5kg weights) = T2 (the 2kg mass).

Example Question #1 : Torque
Two students are balancing on a 10m seesaw. The seesaw is designed so that each side of the seesaw is 5m long. The student on the left weighs 60kg and is standing three meters away from the center. The student on the right weighs 45kg. The seesaw is parallel to the ground. Assume the board that makes the seesaw is massless.
What distance from the center should the student on the right be if they want the seesaw to stay parallel to the ground?
Torque is defined by the equation 


Since the torque must be zero in order for the seesaw to stay parallel (not move), the lighter student on the right must make his torque on the right equal to the torque of the student on the left. We can determine the required distance by setting their torques equal to each other.
Example Question #1 : Torque
Two students are balancing on a 10m seesaw. The seesaw is designed so that each side of the seesaw is 5m long. The student on the left weighs 60kg and is standing three meters away from the center. The student on the right weighs 45kg. The seesaw is parallel to the ground. Assume the board that makes the seesaw is massless.
Imagine that the two students are sitting on the seesaw so that the torque is 
Both students move toward the center by one meter.
Two more students get on the seesaw, each weighing 45kg. They both sit on opposite ends of the seesaw, five meters away from the center.
The heavier student moves forward 1m, while the lighter student moves forward 1.33m.
Another student stands perfectly on the center of the seesaw.
Both students move toward the center by one meter.
Torque, in this case, is dependent on both the force exerted by the students as well as their distances from the point of rotation. As a result, both students moving forward by one meter will cause a nonzero torque on the seesaw. This is because the heavier student's ratio of force and distance will result in less torque on his side than the lighter student.
Example Question #142 : Circular, Rotational, And Harmonic Motion
A 3m beam of negligible weight is balancing in equilibrium with a fulcrum placed 1m from it's left end. If a force of 50N is applied on it's right end, how much force would needs to be applied to the left end?
This a an example of rotational equilibrium involving torque. The formula for torque is 


Since the forces are applied perpendicular to the beam, 
Since the 50N force is twice as far from the fulcrum as the force that must be applied on the left side, it must be half as strong as the force on the left. The force on the left can be found to be 100N.
Example Question #1 : Torque
One side of a seesaw carries a 

For the seesaw to be balanced, the system must be in rotational equilibrium. For this to occur, the torque the same on both sides.
The total torque must be equal on both sides in order for the net torque to be zero.
Substitute the formula for torque into this equation.
Now we can use the given values to solve for the missing mass.
The acceleration form gravity cancels from each term.
Example Question #1091 : Ap Physics 1
Two masses hang below a massless meter stick. Mass 1 is located at the 10cm mark with a weight of 15kg, while mass 2 is located at the 60cm mark with a weight of 30kg. At what point in between the two masses must the string be attached in order to balance the system?
This problem deals with torque and equilibrium. Noting that the string is between the two masses we can use the torque equation of 


x=43, thus the string is placed at the 43cm mark.
Example Question #1 : Rotational, Circular, And Harmonic Motion
A 2kg mass is suspended on a rope that wraps around a frictionless pulley. The pulley is attached to the ceiling and has a mass of 0.01kg and a radius of 0.25m. The other end of the rope is attached to a massless suspended platform, upon which 0.5kg weights may be placed. While the system is initially at equilibrium, the rope is later cut above the weight, and the platform subsequently raised by pulling on the rope.

The rope is cut just above the 2kg mass, and the platform starts to fall. The rope is still wrapped around the pulley. What is the torque around the pulley?
In the instant the rope is cut right above the 2kg mass, the pulley now has net torque in the counterclockwise direction because the platform with the masses is still connected to the rope that winds around the pulley. Knowing that 
Example Question #1 : Torque
Which of these is the correct expression for torque, τ, when θ is the angle at which the force, F, acts around the axis of rotation?
- τ = F cos θ
- τ = F sin θ
- τ = F tan θ
- τ = F cotan θ
- τ = F sec θ
5
2
4
1
3
2
Choice 2 is correct. Think about trying to change a tire…you apply the force on the tire iron as close to perpendicular as possible in order to generate the most force.
Since the sine of 90 degrees is 1, then you are applying the maximum torque you can generate according to the equation τ = F sin θ.
Example Question #1 : Torque
An attraction at a science museum helps teach students about the power of torque. There is a long metal beam that has one pivot point. At one end of the bar hangs a full sedan, and on the other end is a rope at which students can pull down, raising the car off the ground.
The beam is 40 meters long and the pivot point is 5 meters from one end. A car of mass 500kg hangs from the short end of the beam. Neglecting the mass of the beam, what is the minimum mass of a student who can hang from the rope and begin to raise the car off the ground?
More information is needed to answer
We are trying to find what force needs to be applied to the rope to result in a net of zero torque on the beam.
Torque applied by the car:
We can use this to find the mass of a student that will create the same amount of torque while hanging from the rope:
Example Question #121 : Newtonian Mechanics And Motion
Which of the following changes would increase a pendulum's frequency?
Increasing the mass at the end of the pendulum
Increasing the length of the pendulum's string
Increasing the angle of displacement
Decreasing the angle of displacement
Shortening the length of the pendulum's string
Shortening the length of the pendulum's string
The only two factors that affect a pendulum's frequency are the acceleration due to gravity (g) and the length of the pendulum's string (L). This can be seen in the following formula: 
Certified Tutor
All MCAT Physical Resources