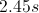This asks us to understand the vector components of velocity. Remember that the final velocity is the hypotenuse of a triangle (solved to be 10m/s in the previous problem), and that by knowing the hypotenuse value we can solve for the horizontal component by using cosine.

v_x = (10m/s)(cos(45^o)) = 7.1m/s

This question also asks us to understand the vector components of velocity. Remember that the final velocity is the hypotenuse of a triangle, and that by knowing the hypotenuse value (solved as 10m/s in a previous problem) we can solve for the vertical component using sine.

v_y = (10m/s)(sin(45^o)) = 7.1m/s

The final and initial velocities are the same if air resistance can be neglected and the start and end positions are at the same height. Kinetic and potential energy must be conserved if there are no frictional forces acting against motion, so the final and initial velocities must be the same.

v_fx = (10 m/s)(cos(45^o)) = 7.1m/s

v_fy = (10 m/s)(sin(45^o)) = 7.1m/s

In order to find the maximum height of the cannonball from the ground, we can use the equation \(\displaystyle \small v_{0}sin(\theta) = \sqrt{2gh}\), with g being the acceleration due to gravity, and h being the height. 

\(\displaystyle \small 120sin(60^{\circ}) = \sqrt{2(10)(h)}\)

\(\displaystyle \small h = 540 m\)

In order to solve for the amount of time, we need to know the vertical initial velocity of the cannonball. This is given by the equation \(\displaystyle \small v_{0}sin(60^{\circ})\). Using the initial velocity of \(\displaystyle \small \small 120\frac{m}{s},\) we determine that the vertical initial velocity is \(\displaystyle \small 104\frac{m}{s}.\)

Knowing this, we can solve the amount of time it will take for the cannon ball to reach its maximum peak, with a velocity of \(\displaystyle \small 0\frac{m}{s}\) using the equation \(\displaystyle \small v = v_{0} + at\)

\(\displaystyle \small 0 = 104\frac{m}{s} + (-10\frac{m}{s^{2}})(t)\)

\(\displaystyle \small t = 10.4 s\)

This is the amount of time it takes for the ball to reach its peak, not the total time it is in the air. Since the ball must drop from the maximum height, we double the time and arrive at the correct answer of 20.8s.

The only acceleration on the cannon ball is done by gravity, which is constant throughout the ball's flight. Since there is no air resistance, the horizontal velocity of the ball is also constant, however, the vertical velocity of the ball is not constant, because the velocity of the ball changes throughout its flight.

It is \(\displaystyle \small 103.9\frac{m}{s}\) at the beginning (\(\displaystyle \small v_{0}sin(60^{\circ})\))and is \(\displaystyle \small 0\frac{m}{s}\) at the maximum height of the cannon ball.

The velocity must be broken down into x (horizontal) and y (vertical) components. We can use the y component to find how high the object gets. To find vertical velocity, v_y, use \(\displaystyle v_y = v_o sin\theta\).

\(\displaystyle v_y = (75 \frac{m}{s})sin 45^o = 53 \frac{m}{s}\)

Next we find how long it takes to reach the top of its trajectory using \(\displaystyle v_f = v_o +at\).

\(\displaystyle 0 \frac{m}{s} = 53 \frac{m}{s} + (-10 \frac{m}{s^2})t\)

 t = 5.3s

Finally, find how high the object goes with \(\displaystyle d = v_ot +\frac{1}{2}at^{2}\).

\(\displaystyle d = (53\frac{m}{s})5.3s + \frac{1}{2}(-10\frac{m}{s^2})(5.3s)^{2} = 140 m\) 

First, find the horizontal (x) and vertical (y) components of the velocity

\(\displaystyle v_x = v_o cos\theta\)

\(\displaystyle v_x = (125 \frac{m}{s}) cos(30^o) = 108\frac{m}{s}\)

\(\displaystyle v_y = v_o sin\theta\)

\(\displaystyle v_y = (125\frac{m}{s})sin(30^o) = 62.5\frac{m}{s}\)

Next, find how long the object is in the air by calculating the time it takes it to reach the top of its path, and doubling that number.

\(\displaystyle v_f = v_o + at\)

\(\displaystyle 0 \frac{m}{s} = 62.5 \frac{m}{s} + (-10 \frac{m}{s^2})t\)

t = 6.25s 

Total time in the air is therefore 12.5s (twice this value).

Finally, find distance traveled my multiplying horizontal velocity and time.

\(\displaystyle d_x = v_x(t)\)

\(\displaystyle d_x = 108 \frac{m}{s} (12.5s) = 1,350 m\)

We can start this problem by determining how much time it takes the box the reach the ground. Since the vertical distance is 30m and we know the angle of the ramp.

\(\displaystyle \frac{1}{2}=\frac{30m}{x}\rightarrow x=60m\)

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity, using the equation \(\displaystyle \small gsin\Theta\).

\(\displaystyle gsin\Theta=(10)sin(60)=8.66\frac{m}{s^2}\)

We can plug these values into the following distance equation and solve for time.

\(\displaystyle \small x = x_{0} - \frac{1}{2}(gsin\Theta )t^{2}\)

\(\displaystyle \small 0 = 60 - \frac{1}{2}(8.66)t^{2}\)

\(\displaystyle \small \small t = 3.72 s\)

Now that we know the acceleration on the box and the time of travel, we can use the equation \(\displaystyle \small v = v_{0} + at\) to solve for the velocity.

\(\displaystyle \small v = 0 + (8.66\frac{m}{s^{2}})(3.72 s) = 32.2 \frac{m}{s}\)

We can start this problem by determining how far the box will travel on the ramp before hitting the ground. Since the vertical distance is 30m and we know the angle of the ramp, we can determine the length of the hypotenuse using the equation \(\displaystyle \small cos(60^{\circ}) = \frac{30}{x}\).

\(\displaystyle \frac{1}{2}=\frac{30m}{x}\rightarrow x=60m\)

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity. Because the box is on a sloped surface, the box will not experience the full acceleration of gravity, but will instead be accelerated at a value of \(\displaystyle \small gsin\Theta\). Since the angle is 60^o, the acceleration on the box is \(\displaystyle \small 8.66 \frac{m}{s^{2}}.\) 

\(\displaystyle gsin\Theta=(10)sin(60)=8.66\frac{m}{s^2}\)

Finally, we can plug these values into the following distance equation and solve for time.

\(\displaystyle \small x = x_{0} - \frac{1}{2}(gsin\Theta )t^{2}\)

\(\displaystyle \small 0 = 60 - \frac{1}{2}(8.66)t^{2}\)

\(\displaystyle \small \small t = 3.72 s\)