All MCAT Physical Resources
Example Questions
Example Question #1 : Thermodynamic Systems And Calorimetry
A scientist prepares an experiment to demonstrate the second law of thermodynamics for a chemistry class. In order to conduct the experiment, the scientist brings the class outside in January and gathers a cup of water and a portable stove.
The temperature outside is –10 degrees Celsius. The scientist asks the students to consider the following when answering his questions:
Gibbs Free Energy Formula:
ΔG = ΔH – TΔS
Liquid-Solid Water Phase Change Reaction:
H2O(l) ⇌ H2O(s) + X
The scientist prepares two scenarios.
Scenario 1:
The scientist buries the cup of water outside in the snow, returns to the classroom with his class for one hour, and the class then checks on the cup. They find that the water has frozen in the cup.
Scenario 2:
The scientist then places the frozen cup of water on the stove and starts the gas. The class finds that the water melts quickly.
After the water melts, the scientist asks the students to consider two hypothetical scenarios as a thought experiment.
Scenario 3:
Once the liquid water at the end of scenario 2 melts completely, the scientist turns off the gas and monitors what happens to the water. Despite being in the cold air, the water never freezes.
Scenario 4:
The scientist takes the frozen water from the end of scenario 1, puts it on the active stove, and the water remains frozen.
In this situation described in the passage, which of the following is true?
The cup of water is the system, and the snow, stove, and remainder of the universe are the surroundings.
The cup of water is the system, and the stove is the surroundings.
The system is all of the universe, except the stove used to input energy.
The cup of water, snow, and stove comprise the system; the universe is the surroundings
The cup of water is the system, and the snow is the surroundings.
The cup of water is the system, and the snow, stove, and remainder of the universe are the surroundings.
The Gibbs Free Energy equation makes use of clearly delineated systems and surroundings. In this example, the water is freezing or melting depending on conditions. This is accompanied by thermal exchanges with other players, such as the snow and stove. Thus, the water is the system, and everything else (technically, everything else in the universe) comprises the surroundings.
Example Question #2 : Thermodynamic Systems And Calorimetry
The combustion of propane is given by the following formula.
If the heats of formation for CO, CO2, H2O, and C3H8 are -110.5 kJ/mol, -393.5 kJ/mol, -241.8 kJ/mol, and -103.85 kJ/mol, respectively, what is the heat of reaction for the combustion of propane?
–1477.9kJ
1477.9kJ
641.95kJ
–641.95kJ
–1477.9kJ
Given the fact that combustion reactions are exothermic, you should expect the heat of reaction to be negative (ruling out two answer choices). The heat of reaction is equal to the heat of formation of the products minus the heat of formation of the reactants. Be sure to refer to the balanced equation for the correct number of moles for each compound.
Oxygen is not included, as it is in elemental form and therefore has a heat of formation equal to zero.
Example Question #41 : Physical Chemistry
The combustion of liquid hexane in air at 298K gives gaseous carbon dioxide and liquid water, as shown in this reaction.




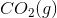


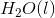

Calculate the 
To calculate the 

Now we can plug in the given values and solve for the enthalpy of reaction.
Example Question #4 : Thermodynamic Systems And Calorimetry
How much energy must a stove transfer to completely transform 

To turn the water into steam, the stove must first raise the temperature of the water, and then provide energy to change the phase. This requires two distinct steps.
Find the energy to raise the temperature of the water using the equation 
Now, we need to find the energy needed to convert the water to a gas. We will use the equation 
Finally, we add the energy for the two steps to find the total energy required.
Example Question #1 : Thermodynamic Systems And Calorimetry

In the above reaction, how much heat will be released if 74.0g of sulfur reacts with excess oxygen? Round to the nearest 10kJ.
Basically, this is a unit conversion problem. Starting with grams of sulfur, convert to moles of sulfur, and finally to kJ of heat released. Note that the given enthalpy of reaction, 
Note that a negative enthalpy of reaction means the process is exothermic and releases heat, while a positive enthalpy of reaction would mean the process is endothermic and absorbs heat.
Example Question #6 : Thermodynamic Systems And Calorimetry
A 50g sample of an unknown substance is heated to 100oC in a tub of boiling water. It is then quickly removed and placed into an insulated jar holding 200mL of water, initially at 20oC. The final equilbrium temperature of the system is 30oC. Approximately, what is the specific heat of this unknown substance?
Specific heat of water is 4.187J/goC.
Density of water is 1g/mL.
Since the system is isolated, the amount of heat transferred away from the unknown substance must equal the heat transferred to the water. To calculate these heats, use
For the water, 
For the unknown substance,
Set these values equal to get cx = 2.39 J/goC, approximately 2.4 J/goC.
Example Question #7 : Thermodynamic Systems And Calorimetry
How much energy is needed to change a 50g ice cube at -30oC into 50g of water at 40oC? Use the above quantities as needed, and round the answer to the nearest kJ.
17kJ
11kJ
7kJ
22kJ
28kJ
28kJ
There are three distinct steps in this transformation: 1) heating the ice from -30oC to 0oC, 2) melting the ice at 0oC, and 3) heating the water from 0oC to 40oC.
When there is a temperature change, we use 

1)
2)
3)
Adding these three pieces together gives the total enthalpy change, which is equal to change in energy.
Example Question #1 : Thermodynamic Systems And Calorimetry
Which term correctly identifies a system in which there is an exchange of heat with the surrounding environment, but no exchange of matter?
Closed system
Isolated system
Open system
Thermodynamic system
Conserved system
Closed system
In a closed system, energy and work can be exchanged with the surrounding area but matter is contained. Consider, for example, a beaker of ice. Heat from the surroundings it transferred to the ice, causing it to melt, but there is no exchange of matter. No external compounds react with the ice and none of the ice leaves the beaker.
In an open system, both heat and matter can be exchanged. In an isolated system neither heat, nor matter is exchanged.
Example Question #61 : Biochemistry, Organic Chemistry, And Other Concepts
You begin an experiment with 


This process can be divided into three stages: the raising of the temperature of the ice, the melting of the ice into water, and the raising of the temperature of the water. The first and third step use the specific heat of the substance to calculate the heat required, while the second step uses the heat of fusion.
Step 1 and 3:
Step 2:
We know the mass of the water, the change in temperature, and the constant values. Using these values, we can sum the heat required for each step to get our final answer.
Example Question #7 : General Thermodynamics
Use the following values for water as needed.
If burning wood releases 



There are two processes requiring added heat in this problem:
1. Raising the temperature of the liquid water from 


2. Boiling the water at a constant temperature of 

To use either of these equation, we need to find the mass of the water using the relation between mass, density, and volume.
Use this mass with the given specific heat and temperatures to find the heat for part 1 of the process.
Then, use the mass with the given heat of vaporization to find the energy needed to convert the water to water vapor.
Sum the energies for step 1 and step 2.
This is the total amount of energy needed from the burning wood. Use stoichiometry to find the grams of wood needed to produce this amount of energy.
Certified Tutor
Certified Tutor
All MCAT Physical Resources



















































































