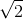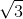All MAP 8th Grade Math Resources
Example Questions
Example Question #1 : Operations And Algebraic Thinking
Solve for
In order to solve for 

For this problem, the first thing we want to do is distribute the 
Next, we can subtract 
Finally, we divide 
Example Question #2 : Operations And Algebraic Thinking
Solve:
In order to solve this problem, we need to recall our exponent rules:
When our base numbers are equal to each other, like in this problem, we can add our exponents together using the following formula:
Let's apply this rule to our problem
Solve for the exponents
We cannot leave this problem in this format because we cannot have a negative exponent. Instead, we can move the base and the exponent to the denominator of a fraction:
Solve the problem
Example Question #3 : Operations And Algebraic Thinking
Use algebra to solve the following system of linear equations:
There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination.
Substitution can be used by solving one of the equations for either 


Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable.
For this problem, substitution makes the most sense because the first equation is already solved for a variable. We can substitute the expression that is equal to 

Next, we need to distribute and combine like terms:
We are solving for the value of 


Then divide both sides by 
Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both 

Now that we have the value of 

Our point of intersection, and the solution to the two system of linear equations is
Example Question #1 : Map 8th Grade Math
Which of the following answer choices displays a rational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
Example Question #2 : Map 8th Grade Math
Which of the following answer choices displays an irrational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
Example Question #3 : Map 8th Grade Math
Solve and leave your answer in scientific notation:
The first step to solving this problem is to combine like terms:
Next, we can solve our two separate multiplication problems starting with the expression on the left:
In order to solve the next expression, we need to recall our exponent rules from a previous lesson:
When our base numbers are equal to each other, like in this problem, we can add our exponents together using the following formula:
Let's apply this rule to our problem:
The question asked us to leave our answer in scientific notation; thus, 
Example Question #4 : Map 8th Grade Math
Observe the location of the black and orange angles on the provided coordinate plane and identify which of the following transformations—rotation, translation, or reflection—the black angle has undergone in order to reach the position of the orange angle. Select the answer that provides the correct transformation shown in the provided image.

A 
A translation to the left
A translation down
A reflection over the x-axis
A 
First, let's define the possible transformations.
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
In the images from the question, notice that the black angle rotates 

The transformation can't be a reflection over the x-axis because the orange angle didn't flip over the x-axis.
The transformation can't be a translation because the angle changes direction, which does not happened when you simply move or slide an angle or image.
Example Question #5 : Map 8th Grade Math
What is the scale of the dilation that the blue rectangle underwent to get the purple rectangle in the image provided?

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle doubles in the purple rectangle, from the blue rectangle; thus the scale of the dilation is
Example Question #6 : Map 8th Grade Math
Calculate the volume of the cone provided. Round the answer to the nearest hundredth.

In order to solve this problem, we need to recall the formula used to calculate the volume of a cone:
Now that we have this formula, we can substitute in the given values and solve:
Example Question #7 : Map 8th Grade Math
The scatter plot provided displays a group of students' test scores versus the number of missing assignments the students have. Based on plot, select the best answer that describes the direction of the points.

A negative, non linear association
A negative, linear association
A positive, linear association
A positive, nonlinear association
A negative, linear association
The data points in the scatter plot move up the y-axis as the x-axis decreases; thus the data points show a negative association. Also, the data points do not curve, or go up and down, but gradually decreased; thus the scatter plot shows a linear association. We could even draw a "best fit" line:

Certified Tutor
All MAP 8th Grade Math Resources









![\frac{\begin{array}[b]{r}32=4x+160\\ -160\ \ \ \ \ \ \ \ \ \ \-160 \end{array}}{\\\\-128=4x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/951901/gif.latex)






















![\frac{\begin{array}[b]{r}15y+3=-27\\ \ -3\ \ \ \ -3\end{array}}{\\\\15y=-30}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/956490/gif.latex)