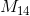One way to calculate the determinant of a three-by-three matrix is as follows:

Choose a row  or column  of the matrix, multiply each element of the row or column  by its corresponding cofactor , and add the products. The best row or column to choose is Row 1, which has two zeroes; the determinant will be

Examining , we see that  , so the expression simplifies to 

,

that is, 4 times the cofactor .

To find cofactor , first find the minor , the determinant of the matrix formed by striking out Row 1 and Column 1, as seen below:

,  which can be calculated by taking the product of the upper-left and lower-right elements and subtracting that of the other two:

Cofactor  can be calculated from a minor  using the formula

so, setting :

The determinant of  is 

regardless of the value of .

The minor of a matrix  is the determinant of the matrix formed by striking out Row  and Column . By definition, the corresponding cofactor  can be calculated from this minor using the formula

Set ; the formula becomes

.

Therefore, the cofactor  must be equal to the opposite of the minor .

The minor of a matrix  is the determinant of the matrix formed by striking out Row  and Column . By definition, the corresponding cofactor  can be calculated from this minor using the formula

Set ; the formula becomes

,

making the quantities equal.

This is not easy to prove in a nutshell, but it can be believed by examining a few examples.

For instance

 .

And swapping the 2nd and the 4th row gives

.

So the determinants are negatives of each other. (Both determinants were evaluated using a calculator.)

We cannot deduce anything about how the determinant of a multiple of  changes without knowing the size of . In general , where  is the size of the (square) matrix .

In our case , which varies depending on the size of the matrix in question.

The determinant of the product of two matrices is equal to the product of the individual determinants, so

By a trigonometric identity, 

, or , so, setting :

.

A way to simplify this problem is to translate each of the points using the transformation 

.

This translates the points as follows:

Replace  with  for the sake of simplicity.

The determinant equation becomes

The determinant can be calculated by multiplying each entry in one row or column by its corresponding cofactor, then adding the products.The easiest row or column to choose is the second row, which has only one nonzero entry. This is equal to 

 is equal to , 

Minor is the determinant of the matrix formed by the deletion of the second row and the fourth column; this determinant is

The determinant of a three-by-three matrix can be found by adding the upper-left to lower-right products and subtracting the upper-right to lower-left products, as shown:

Set this determinant equal to 0. The equation of the plane in terms of  is 

Substituting back for these variables, the equation becomes

,

the correct response.

Replace the first three elements in each of the last three rows with the given coordinates of the points:

The determinant can be calculated by multiplying each entry in one row or column by its corresponding cofactor, then adding the products.The easiest row or column to choose is the second row, which has only one nonzero entry. This is equal to 

 is equal to , 

Minor  is the determinant of the matrix formed by the deletion of the second row and the fourth column; this determinant is

The determinant of a three-by-three matrix can be found by adding the upper-left to lower-right products and subtracting the upper-right to lower-left products, as shown:

Set this determinant equal to 0. The equation of the plane is 

.

The determinant of the product of matrices is equal to the product of the individual determinants; also, the determinant of the inverse of a matrix is the reciprocal of the determinant of the original matrix. Therefore, 

The statement is true.

The determinant of the product of matrices is equal to the product of the individual determinants; also, the determinant of the transpose of a matrix is equal to that of the original matrix. It follows that 

Therefore,  is only true if , or, equivalently, if . The statement is false.