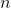Call Now to Set Up Tutoring:

(888) 888-0446

Linear Algebra : Matrix-Matrix Product

Study concepts, example questions & explanations for Linear Algebra

Create An Account

All Linear Algebra Resources

4 Diagnostic Tests 108 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : Matrix Matrix Product

Find the product $A \times B$ .

$A=\begin{bmatrix} -1& 2\\ 4& 3 \\ 5& -1 \end{bmatrix}$ , $B=\begin{bmatrix} 7& -1\\ -2& 5 \end{bmatrix}$

Possible Answers:

$A \times B$ cannot be multiplied

$A \times B=\begin{bmatrix} -7& -2\\ -8& 15 \\ 5& -1 \end{bmatrix}$

$A \times B=\begin{bmatrix} 7& -1\\ -2& 5 \\ 5& -1 \end{bmatrix}$

$A \times B=\begin{bmatrix} -11& 11\\ 22& 11\\ 37& 10 \end{bmatrix}$

Correct answer:

$A \times B=\begin{bmatrix} -11& 11\\ 22& 11\\ 37& 10 \end{bmatrix}$

Explanation:

If is an $(m\times n)$ matrix and is an $(r\times s)$ matrix,

$(A\times B)$ can only be multiplied if n=r , or the number of columns in equals the number of rows in . Otherwise there is a mismatch, and the two matrices can not be multiplied. $(A\times B)$ will be an $(m\times s)$ matrix

Since is a $3\times2$ matrix and is a $2\times2$ matrix, then $(A\times B)$ can be multiplied and will have the dimensions $3\times2$ .

$A \times B=\begin{bmatrix} ab_{11}& ab_{12}\\ ab_{21}& ab_{22}\\ ab_{31}& ab_{32} \end{bmatrix}$

To find the product $A \times B$ , you must find the dot product of the rows of and the columns of

$A=\begin{bmatrix} -1& 2\\ 4& 3 \\ 5& -1 \end{bmatrix}$ , $B=\begin{bmatrix} 7& -1\\ -2& 5 \end{bmatrix}$

$A \times B=\begin{bmatrix} ab_{11}& ab_{12}\\ ab_{21}& ab_{22}\\ ab_{31}& ab_{32} \end{bmatrix}$

We find $ab_{11}$ by finding the dot product of the row of and column of .

$ab_{11}=(-1)(7)+(2)(-2)=-7-4=-11$

We find $ab_{12}$ by finding the dot product of the row of and column of .

$ab_{12}=(-1)(-1)+(2)(5)=1+10=11$

We use the same method to find the rest of the matrix values

$ab_{21}=(4)(7)+(3)(-2)=28-6=22$

$ab_{22}=(4)(-1)+(3)(5)=-4+15=11$

$ab_{31}=(5)(7)+(-1)(-2)=35+2=37$

$ab_{32}=(5)(-1)+(-1)(5)=-5-5=10$

$A \times B=\begin{bmatrix} -11& 11\\ 22& 11\\ 37& 10 \end{bmatrix}$

Report an Error

Example Question #42 : Matrices

Find the product $A \times B$ .

$A=\begin{bmatrix} -1& 2 &5\\ 4& 3 &1 \end{bmatrix}$ , $B=\begin{bmatrix} 7& -1\\ -2& 5 \end{bmatrix}$

Possible Answers:

$A \times B=\begin{bmatrix} -7& -2 \\ -8& 15 \end{bmatrix}$

$A \times B=\begin{bmatrix} 6& 1 &5\\ 2& 8 &1 \end{bmatrix}$

$A \times B$ cannot be multiplied.

$A \times B=\begin{bmatrix} -7& -2 &5\\ -8& 15 &1 \end{bmatrix}$

Correct answer:

$A \times B$ cannot be multiplied.

Explanation:

If is an $(m\times n)$ matrix and is an $(r\times s)$ matrix,

Since is a $2\times3$ matrix and is a $2\times2$ matrix, $n\neq r$ so $(A\times B)$ cannot be multiplied.

Report an Error

Example Question #723 : Linear Algebra

Find the product $A \times B$ .

$A=\begin{bmatrix} -1 &5\\ 4 &1 \end{bmatrix}$ , $B=\begin{bmatrix} 7& -1& 0\\ -2& 5&8 \end{bmatrix}$

Possible Answers:

$A \times B=\begin{bmatrix} -7& -5& 0\\ -8& 5&8 \end{bmatrix}$

$A \times B=\begin{bmatrix} -1& 5& 0\\ 4& 1&8 \end{bmatrix}$

$A \times B$ cannot be multiplied

$A \times B=\begin{bmatrix} -17& 26& 40\\ 26& 1&8 \end{bmatrix}$

Correct answer:

$A \times B=\begin{bmatrix} -17& 26& 40\\ 26& 1&8 \end{bmatrix}$

Explanation:

If is an $(m\times n)$ matrix and is an $(r\times s)$ matrix,

Since is a $2\times2$ matrix and is a $2\times3$ matrix, then $(A\times B)$ can be multiplied and will have the dimensions $2\times3$ .

$A \times B=\begin{bmatrix} ab_{11}& ab_{12}& ab_{13}\\ ab_{21}& ab_{22}& ab_{23} \end{bmatrix}$

To find the product $A \times B$ , you must find the dot product of the rows of and the columns of

$A=\begin{bmatrix} -1 &5\\ 4 &1 \end{bmatrix}$ , $B=\begin{bmatrix} 7& -1& 0\\ -2& 5&8 \end{bmatrix}$

$A \times B=\begin{bmatrix} ab_{11}& ab_{12}& ab_{13}\\ ab_{21}& ab_{22}& ab_{23} \end{bmatrix}$

We find $ab_{11}$ by finding the dot product of the row of and column of .

$ab_{11}=(-1)(7)+(5)(-2)=-7-10=-17$

We find $ab_{12}$ by finding the dot product of the row of and column of .

$ab_{12}=(-1)(-1)+(5)(5)=1+25=26$

We use the same method to find the rest of the matrix values

$ab_{13}=(-1)(0)+(5)(8)=0+40=40$

$ab_{21}=(4)(7)+(1)(-2)=28-2=26$

$ab_{22}=(4)(-1)+(1)(5)=-4+5=1$

$ab_{23}=(4)(0)+(1)(8)=0+8=8$

$A \times B=\begin{bmatrix} -17& 26& 40\\ 26& 1&8 \end{bmatrix}$

Report an Error

Example Question #724 : Linear Algebra

Find the product $A \times B$ .

$A=\begin{bmatrix} -1 &5&2\\ 4 &-4&5 \end{bmatrix}$ , $B=\begin{bmatrix} 7& -1& 0\\ -2& 5&8\\ 1& 2&4 \end{bmatrix}$

Possible Answers:

$A \times B=\begin{bmatrix} -15& 30& 48\\ 41& -14&-12 \end{bmatrix}$

$A \times B=\begin{bmatrix} -7 &-5&0\\ -8 &-20&40 \end{bmatrix}$

$A \times B$ cannot be multiplied

$A \times B=\begin{bmatrix} 7& -1& 0\\ -2& 5&8 \end{bmatrix}$

Correct answer:

$A \times B=\begin{bmatrix} -15& 30& 48\\ 41& -14&-12 \end{bmatrix}$

Explanation:

If is an $(m\times n)$ matrix and is an $(r\times s)$ matrix,

Since is a $2\times3$ matrix and is a $3\times3$ matrix, then $(A\times B)$ can be multiplied and will have the dimensions $2\times3$ .

$A \times B=\begin{bmatrix} ab_{11}& ab_{12}& ab_{13}\\ ab_{21}& ab_{22}& ab_{23} \end{bmatrix}$

To find the product $A \times B$ , you must find the dot product of the rows of and the columns of

$A=\begin{bmatrix} -1 &5&2\\ 4 &-4&5 \end{bmatrix}$ , $B=\begin{bmatrix} 7& -1& 0\\ -2& 5&8\\ 1& 2&4 \end{bmatrix}$

$A \times B=\begin{bmatrix} ab_{11}& ab_{12}& ab_{13}\\ ab_{21}& ab_{22}& ab_{23} \end{bmatrix}$

We find $ab_{11}$ by finding the dot product of the row of and column of .

$ab_{11}=(-1)(7)+(5)(-2)+(2)(1)=-7-10+2=-15$

We find $ab_{12}$ by finding the dot product of the row of and column of .

$ab_{12}=(-1)(-1)+(5)(5)+(2)(2)=1+25+4=30$

We use the same method to find the rest of the matrix values

$ab_{13}=(-1)(0)+(5)(8)+(2)(4)=0+40+8=48$

$ab_{21}=(4)(7)+(-4)(-2)+(5)(1)=28+8+5=41$

$ab_{22}=(4)(-1)+(-4)(5)+(5)(2)=-4-20+10=-14$

$ab_{23}=(4)(0)+(-4)(8)+(5)(4)=0-32+20=-12$

$A \times B=\begin{bmatrix} -15& 30& 48\\ 41& -14&-12 \end{bmatrix}$

Report an Error

Example Question #42 : Matrices

Find the product $A \times B$ .

$A=\begin{bmatrix} -1 &5&2\\ 4 &-4&5 \end{bmatrix}$ , $B=\begin{bmatrix} 2 &-1&5\\ 0 &-7&4 \end{bmatrix}$

Possible Answers:

$A \times B=\begin{bmatrix} -3 &6&-3\\ 4 &3&1 \end{bmatrix}$

$A \times B=\begin{bmatrix} -2 &-5&10\\ 0 &28&20 \end{bmatrix}$

$A \times B$ cannot be multiplied.

$A \times B=\begin{bmatrix} 1 &4&7\\ 0 &-7&9 \end{bmatrix}$

Correct answer:

$A \times B$ cannot be multiplied.

Explanation:

If is an $(m\times n)$ matrix and is an $(r\times s)$ matrix,

Since is a $2\times3$ matrix and is a $2\times3$ matrix, $n\neq r$ so $(A\times B)$ cannot be multiplied.

Report an Error

Example Question #731 : Linear Algebra

$A = \begin{bmatrix} \frac{1}{4} & \frac{\sqrt{3}}{4} \\ \\ \frac{\sqrt{3}}{4} & \frac{3}{4} \end{bmatrix}$

True or false:

is an example of an idempotent matrix.

Possible Answers:

False

True

Correct answer:

True

Explanation:

is an idempotent matrix, by definition, if $A^{2} = A$ . Multiply by itself by multiplying rows by columns - multiplying elements in corresponding positions and adding the products:

$A ^{2}= \begin{bmatrix} \frac{1}{4} & \frac{\sqrt{3}}{4} \\ \\ \frac{\sqrt{3}}{4} & \frac{3}{4} \end{bmatrix} \begin{bmatrix} \frac{1}{4} & \frac{\sqrt{3}}{4} \\ \\ \frac{\sqrt{3}}{4} & \frac{3}{4} \end{bmatrix}$

$= \begin{bmatrix} \frac{1}{4} \cdot \frac{1}{4} + \frac{\sqrt{3}}{4} \cdot \frac{\sqrt{3}}{4} & \frac{1}{4} \cdot \frac{\sqrt{3}}{4} + \frac{\sqrt{3}}{4} \cdot \frac{3}{4} \\ \\\ \ \frac{\sqrt{3}}{4} \cdot \frac{1}{4} + \frac{3}{4} \cdot \frac{\sqrt{3}}{4} & \frac{\sqrt{3}}{4} \cdot \frac{\sqrt{3}}{4} + \frac{3}{4} \cdot \frac{3}{4} \end{bmatrix}$

$= \begin{bmatrix} \frac{1}{16} + \frac{ 3}{16} & \frac{\sqrt{3}}{16} + \frac{3\sqrt{3}}{16} \\ \\\ \ \frac{\sqrt{3}}{16} +\frac{3\sqrt{3}}{16} & \frac{3}{16} + \frac{9}{16} \end{bmatrix}$

$= \begin{bmatrix} \frac{1}{4} & \frac{\sqrt{3}}{4} \\ \\ \frac{\sqrt{3}}{4} & \frac{3}{4} \end{bmatrix} =A$ .

$A^{2} = A$ , making idempotent.

Report an Error

Example Question #732 : Linear Algebra

$A = \begin{bmatrix} 0 &- 1 \\ 1 & 0 \end{bmatrix}$

True or false:

is an example of an idempotent matrix.

Possible Answers:

False

True

Correct answer:

False

Explanation:

is an idempotent matrix, by definition, if $A^{2} = A$ . Multiply by itself by multiplying rows by columns - multiplying elements in corresponding positions and adding the products:

$A^{2} = \begin{bmatrix} 0 &- 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 0 &- 1 \\ 1 & 0 \end{bmatrix}$

$= \begin{bmatrix} 0(0) + (-1) (1) & 0 (-1)+ (-1) (0) \\ 1(0) + 0 (1) & 1(-1)+ 0(0) \end{bmatrix}$

$= \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$

$A^{2} \ne A$ , so is not idempotent.

Report an Error

Example Question #733 : Linear Algebra

For any given value , how many $n \times n$ nonsingular idempotent matrices exist?

Possible Answers:

Zero

Infinitely many

One

Two

Correct answer:

One

Explanation:

is nonsingular, by definition, if it has an inverse - that is, if $A^{-1}$ exists. is an idempotent matrix, by definition, if

$A^{2} = A$

Premultiplying both sides of the equation by $A^{-1}$ , we get

$A^{-1}(A^{2}) = A^{-1}A$

$A^{-1}(AA )= I$ ,

where is the $n \times n$ identity matrix.

Matrix multiplication is associative, so

$(A^{-1}A)A = I$

IA = I

A = I .

Therefore, the only nonsingular idempotent matrix of a given dimension $n \times n$ is the identity.

Report an Error

Example Question #734 : Linear Algebra

Markov 2

The above diagram shows a board for a game of chance. A player moves according to the flip of a fair coin, depending on his current location. For example, if he is on the green square, he will move to the orange square if the coin comes up heads, and to the pink square if it comes up tails.

Construct a stochastic matrix that models this game, with the rows/columns representing, in order, the orange, pink, blue, and green squares.

Possible Answers:

$\begin{bmatrix} 0.5 & 0.5 & 0&0 \\ 0.5 &0 & 0.5 & 0\\ 0 & 0.5 &0 & 0.5 \\ 0.5 & 0 .5 & 0 & 0 \end{bmatrix}$

$\begin{bmatrix} 0 & 0.5 & 0&0.5 \\ 0.5 &0 & 0.5& 0 \\ 0 & 0.5 &0 & 0.5 \\ 0.5 & 0 & 0.5 & 0 \end{bmatrix}$

$\begin{bmatrix} 0.5 & 0.5 & 0&0.5 \\ 0.5 &0 & 0.5 & 0.5\\ 0 & 0.5 &0 & 0 \\ 0 & 0 & 0.5 & 0 \end{bmatrix}$

$\begin{bmatrix} 0.5 & 0 & 0.5&0.5 \\ 0.5 &0.5 & 0 & 0.5\\ 0 & 0 &0.5 & 0 \\ 0 & 0.5 & 0 & 0 \end{bmatrix}$

$\begin{bmatrix} 0.5 &0 & 0.5& 0 \\ 0 & 0.5 &0 & 0.5 \\ 0.5 & 0 & 0.5 & 0 \\ 0 & 0.5 & 0&0.5 \end{bmatrix}$

Correct answer:

$\begin{bmatrix} 0.5 & 0.5 & 0&0.5 \\ 0.5 &0 & 0.5 & 0.5\\ 0 & 0.5 &0 & 0 \\ 0 & 0 & 0.5 & 0 \end{bmatrix}$

Explanation:

Since the coin is fair, each outcome will come up with probability 0.5. Therefore, a player on orange end up on orange or pink with 0.5 probability each; a player on pink will end up on orange or blue with probability 0.5 each; a player on blue will end up on pink or green with probability 0.5 each; and a player on green will end up on orange or pink with probability 0.5 each. The matrix that models this is

$\begin{bmatrix} 0.5 & 0.5 & 0&0.5 \\ 0.5 &0 & 0.5 & 0.5\\ 0 & 0.5 &0 & 0 \\ 0 & 0 & 0.5 & 0 \end{bmatrix}$ .

Report an Error

Example Question #735 : Linear Algebra

Markov 2

It is recommended that you use a calculator with matrix arithmetic capability for this problem.

The player agrees to start on the pink square. Which square is he most likely to end up on after eight moves?

Possible Answers:

Orange

Pink

Green

Blue

Correct answer:

Orange

Explanation:

$P = \begin{bmatrix} 0.5 & 0.5 & 0&0.5 \\ 0.5 &0 & 0.5 & 0.5\\ 0 & 0.5 &0 & 0 \\ 0 & 0 & 0.5 & 0 \end{bmatrix}$ .

The matrix that models the probabilities that the player will end up on a given square, given that he starts on a particular square, is $P^{8}$ , which through calculation is

$P^{8} = \begin{bmatrix} 0.4180 & 0.4141&0.4180 &0.4180 \\ 0.3320 &0.3359 &0.3320 &0.3320 \\ 0.1680 & 0.1641 & 0.1680 &0.1680 \\ 0.0820 & 0.0859 &0.0820 & 0.0820 \end{bmatrix}$

Since the player is starting on pink, examine the second column; the greatest entry is in the second row, which represents ending up on orange.

Report an Error

View Linear Algebra Tutors

Chelsea
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Physics. The University of Texas at Dallas, Master of Science, Bioinf...

View Linear Algebra Tutors

Nima
Certified Tutor

Sahand University of Technology, Master of Science, Electrical Engineering. Institut national de la recherche scientifique, D...

View Linear Algebra Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

All Linear Algebra Resources

4 Diagnostic Tests 108 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Chicago, SSAT Tutors in Phoenix, LSAT Tutors in Boston, Algebra Tutors in Atlanta, Physics Tutors in Seattle, Math Tutors in Phoenix, French Tutors in Los Angeles, ACT Tutors in Atlanta, Algebra Tutors in New York City, Algebra Tutors in Chicago

Popular Courses & Classes

GRE Courses & Classes in New York City, ACT Courses & Classes in Boston, ACT Courses & Classes in Philadelphia, ACT Courses & Classes in Houston, Spanish Courses & Classes in Los Angeles, SAT Courses & Classes in Washington DC, GRE Courses & Classes in Phoenix, MCAT Courses & Classes in San Diego, ACT Courses & Classes in New York City, MCAT Courses & Classes in Washington DC

Popular Test Prep

GRE Test Prep in Miami, SAT Test Prep in Philadelphia, LSAT Test Prep in Los Angeles, GMAT Test Prep in New York City, ACT Test Prep in New York City, MCAT Test Prep in Denver, GMAT Test Prep in Phoenix, GMAT Test Prep in Philadelphia, SAT Test Prep in Seattle, SSAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Linear Algebra : Matrix-Matrix Product

Study concepts, example questions & explanations for Linear Algebra

All Linear Algebra Resources

Example Questions

Example Question #41 : Matrix Matrix Product

Example Question #42 : Matrices

Example Question #723 : Linear Algebra

Example Question #724 : Linear Algebra

Example Question #42 : Matrices

Example Question #731 : Linear Algebra

Example Question #732 : Linear Algebra

Example Question #733 : Linear Algebra

Example Question #734 : Linear Algebra

Example Question #735 : Linear Algebra

All Linear Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: