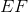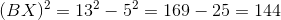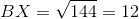All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #9 : Right Triangles
In Square 








Which is the greater quantity?
(a)
(b)
It cannot be determined which of (a) and (b) is greater
(b) is the greater quantity
(a) and (b) are equal
(a) is the greater quantity
(b) is the greater quantity
The figure referenced is below:
For the sake of simplicity, assume that the square has sides of length 4. The following reasoning is independent of the actual lengths, and the reason for choosing 4 will become apparent in the explanation.





Also, 






Example Question #10 : Right Triangles

Figure NOT drawn to scale.
In the above figure, 
What is the length of 
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,

Their corresponding sides are in proportion, so, setting the ratios of the hypotenuses to the short legs equal to each other,
Example Question #41 : Plane Geometry

Figure NOT drawn to scale.
In the above figure, 
What is the length of 
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,

Their corresponding sides are in proportion, so, setting the ratios of the long legs to the short legs equal to each other,
By the Pythagorean Theorem.
The proportion statement becomes
Example Question #41 : Triangles
Given: 



Which is the greater quantity?
(a)
(b)
(a) is the greater quantity
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
(a) is the greater quantity
The measure of the angle formed by the two shorter sides of a triangle can be determined to be acute, right, or obtuse by comparing the sum of the squares of those lengths to the square of the length of the opposite side. We compare:


Example Question #43 : Plane Geometry

Figure NOT drawn to scale.
In the above figure, 
What is the length of 
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,

Their corresponding sides are in proportion, so, setting the ratios of the hypotenuses to the short legs equal to each other,
Example Question #41 : Geometry





Which is the greater quantity?
(a)
(b)
(a) and (b) are equal.
(a) is greater.
(b) is greater.
It is impossible to tell from the information given.
(a) is greater.
Each right triangle is a 
Since 



By the 



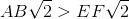
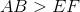
Example Question #2 : How To Find If Triangles Are Similar

Figure NOT drawn to scale.
In the above figure, 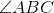
What is the ratio of the area of 
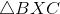
12 to 5
13 to 5
144 to 25
169 to 25
144 to 25
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller, similar triangles.
The similarity ratio of 


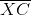

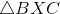
The similarity ratio is therefore

The ratio of the areas is the square of this ratio:

Example Question #11 : Right Triangles

Refer to the above right triangle. Which of the following is equal to 
By the Pythagorean Theorem,
Example Question #47 : Plane Geometry
Given 

Which is the greater quantity?
(a)
(b)
(b) is greater.
It is impossible to tell from the information given.
(a) and (b) are equal.
(a) is greater.
(a) and (b) are equal.
The sum of the measures of the angles of a triangle is , so:
This is a 


Example Question #48 : Plane Geometry

Give the length of one leg of an isosceles right triangle whose area is the same as the right triangle in the above diagram.
The area of a triangle is half the product of its height and its base; in a right triangle, the legs, being perpendicular, can serve as these quantites.
The triangle in the diagram has area

An isosceles right triangle has two legs of the same length, which we will call 

All ISEE Upper Level Quantitative Resources