ISEE Upper Level Quantitative : Triangles
Study concepts, example questions & explanations for ISEE Upper Level Quantitative
All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #51 : Triangles
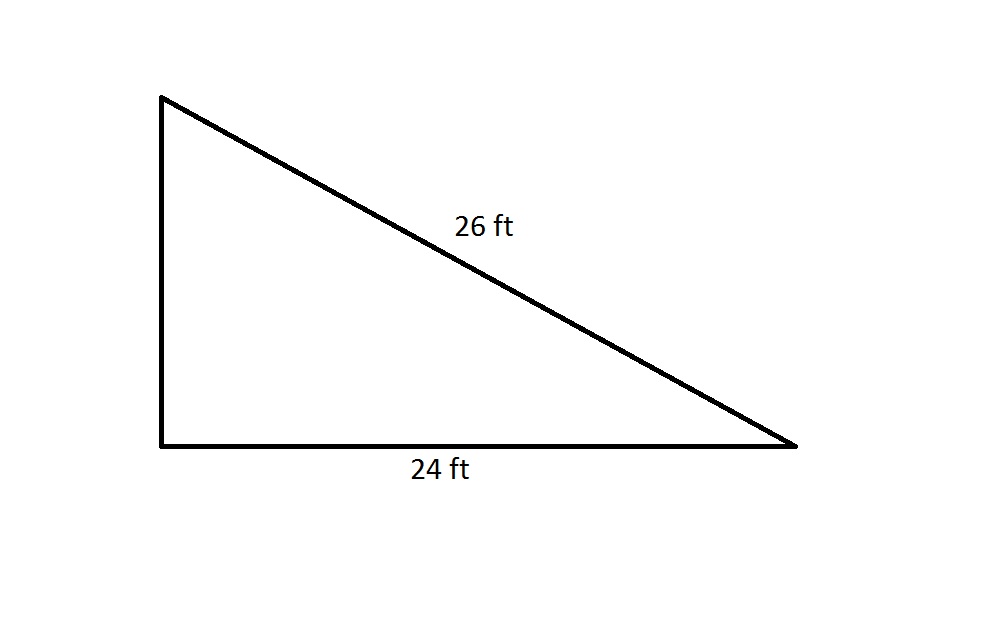
The perimeter of a regular octagon is 20% greater than that of the above right triangle. Which is the greater quantity?
(A) The length of one side of the octagon
(B) 3 yards
(A) and (B) are equal
(A) is greater
It is impossible to determine which is greater from the information given
(B) is greater
(A) and (B) are equal
By the Pythagorean Theorem, the shorter leg has length
The perimeter of the right triangle is therefore
The octagon has perimeter 20% greater than this, or
A regular octagon has eight sides of equal length, so each side of this octagon has length
Example Question #2 : How To Find The Length Of The Side Of A Right Triangle
The area of a square is equal to that of the above right triangle. Which is the greater quantity?
(A) The sidelength of the square
(B) 4 yards
(B) is greater
(A) is greater
It is impossible to determine which is greater from the information given
(A) and (B) are equal
(B) is greater
By the Pythagorean Theorem, the shorter leg has length
The area of a triangle is equal to half the product of its base and height; for a right triangle, the legs can serve as these. The area of the above right triangle is
The sidelength is the square root of this; 
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
Figure NOT drawn to scale.
Refer to the above triangle. Which is the greater quantity?
(a)
(b) 108
(a) and (b) are equal
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) is the greater quantity
(b) is the greater quantity
We can compare these numbers by comparing their squares.
By the Pythagorean Theorem,
Also,
Example Question #52 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
Consider a triangle, 
(a) 55
(b)
(a) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
(b) is the greater quantity
(b) is the greater quantity
Suppose 
By the Converse of the Pythagorean Theorem, a triangle is right if and only if the sum of the squares of the lengths of the smallest two sides is equal to the square of the longest side. Compare the quantities 
Therefore, if
However, 
Example Question #51 : Triangles
Which is the greater quantity?
(a) The perimeter of
(b) The perimeter of
(a) is greater.
(a) and (b) are equal.
It is impossible to tell from the information given.
(b) is greater.
It is impossible to tell from the information given.
No information is given about the legs of either triangle; therefore, no information about their perimeters can be deduced.
Example Question #53 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
Note: Figure NOT drawn to scale
Refer to the above triangle. Starting at point A, an insect walks clockwise along the sides of the triangle until he has walked 75% of the length of 
By the Pythagorean Theorem, the distance from B to C, which we will call 
The perimeter of the triangle is
The insect traveled the entirety of the hypotenuse, which is 13 units long, and 75% of the longer leg, which adds 75% of 12, or 
Example Question #53 : Plane Geometry
Refer to the above diagram, in which 
(a) Four times the perimeter of
(b) Three times the perimeter of
It is impossible to determine which is greater from the information given
(a) and (b) are equal
(b) is the greater quantity
(a) is the greater quantity
(a) and (b) are equal
The altitude of a right triangle from the vertex of its right angle - which, here, is 
making this the similarity ratio. The ratio of the perimeters of two similar triangles is the same as their similarity ratio; therefore, if 
Multiply both sides by 3:
Three times the perimeter of 
Example Question #54 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
Quantity A: The hypotenuse of a right triangle with sides 
Quantity B: The height of a triangle with an area of 
Quantity B is greater.
The two quantities are equal.
The relationship of the quantities cannot be determined.
Quantity A is greater.
The two quantities are equal.
Quantity A: This is the special 
Quantity B: This triangle has an area of 
Quantity A and Quantity B are equal.
Example Question #52 : Triangles
Note: Figure NOT drawn to scale.
Refer to the above figure.
Which is the greater quantity?
(a)
(b)
It is impossible to tell from the information given.
(a) is greater.
(a) and (b) are equal.
(b) is greater.
(a) and (b) are equal.
Since the shorter leg of the right triangle is half the hypotenuse, the triangle is a 
Example Question #53 : Triangles
Right triangle 
Which is the greater quantity?
(a)
(b)
(a) and (b) are equal
(a) is greater
(b) is greater
It is impossible to tell from the information given
(a) is greater
The degree measures of the acute angles of a right triangle total 90, so we solve for 
(a)
(b)
All ISEE Upper Level Quantitative Resources
