Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Quantitative : ISEE Upper Level (grades 9-12) Quantitative Reasoning

Study concepts, example questions & explanations for ISEE Upper Level Quantitative

Create An Account

All ISEE Upper Level Quantitative Resources

8 Diagnostic Tests 234 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Area Of An Equilateral Triangle

$\Delta ABC$ is an equilateral triangle. Points D,E,F are the midpoints of $\overline{AB},\overline{BC},\overline{AC}$ , respectively. $\Delta DEF$ is constructed.

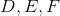
Which is the greater quantity?

(a) The area of $\Delta ABC$

(b) Twice the area of $\Delta DEF$

Possible Answers:

(b) is greater.

(a) and (b) are equal.

It is impossible to tell from the information given.

(a) is greater.

Correct answer:

(a) is greater.

Explanation:

If segments are constructed in which the endpoints form the midpoints of the sides of a triangle, then four triangles, congruent to each other and similar to the larger triangle, are formed. Therefore, one of these triangles - specifically, $\Delta DEF$ - would have one-fourth the area of $\Delta ABC$ . This means $\Delta ABC$ has more than twice the area of $\Delta DEF$ .

Note that the fact that the triangle is equilateral is irrelevant.

Report an Error

Example Question #2 : Equilateral Triangles

Which of the following could be the three sidelengths of an equilateral triangle?

Possible Answers:

$2 \textrm{ yd, } 84 \textrm{ in, }7\textrm{ ft}$

$\frac{2}{3} \textrm{ yd, } 24 \textrm{ in, }2\textrm{ ft}$

$1\frac{1}{2} \textrm{ yd, } 50 \textrm{ in, }4\textrm{ ft}$

$1\frac{2}{3} \textrm{ yd, } 48 \textrm{ in, }4\textrm{ ft}$

$1\frac{1}{3} \textrm{ yd, } 48 \textrm{ in, }5\textrm{ ft}$

Correct answer:

$\frac{2}{3} \textrm{ yd, } 24 \textrm{ in, }2\textrm{ ft}$

Explanation:

By definition, an equilateral triangle has three sides of equal length. We can identify the equilateral triangle by converting the given sidelengths to the same units and comparing them.

We can eliminate the following by showing that at least two sidelengths differ.

$2 \textrm{ yd, } 84 \textrm{ in, }7\textrm{ ft}$

2 yards = $2 \times 3 = 6$ feet.

Two sides have lengths 6 feet and 7 feet, so we can eliminate this choice.

$1\frac{1}{2} \textrm{ yd, } 50 \textrm{ in, }4\textrm{ ft}$

4 feet = $4 \times 12 = 48$ inches

Two sides have lengths 48 inches and 50 inches, so we can eliminate this choice.

$1\frac{1}{3} \textrm{ yd, } 48 \textrm{ in, }5\textrm{ ft}$

5 feet = $5 \times 12 = 60$ inches

Two sides have lengths 48 inches and 60 inches, so we can eliminate this choice.

$1\frac{2}{3} \textrm{ yd, } 48 \textrm{ in, }4\textrm{ ft}$

$1\frac{2}{3}$ yards = $1\frac{2}{3} \times 3 = 5$ feet

Two sides have lengths 4 feet and 5 feet, so we can eliminate this choice.

$\frac{2}{3} \textrm{ yd, } 24 \textrm{ in, }2\textrm{ ft}$

$\frac{2}{3}$ yards = $\frac{2}{3} \times3 = 2$ feet = $2 \times 12 = 24$ inches

All three sides have the same length, making this the triangle equilateral. This choice is correct.

Report an Error

Example Question #1 : Right Triangles

What is the hypotenuse of a right triangle with sides 5 and 8?

Possible Answers:

√89

5√4

Correct answer:

√89

Explanation:

Because this is a right triangle, we can use the Pythagorean Theorem which says a² + b² = c², or the squares of the two sides of a right triangle must equal the square of the hypotenuse. Here we have a = 5 and b = 8.

a² + b² = c²

5² + 8² = c²

25 + 64 = c²

89 = c²

c = √89

Report an Error

Example Question #2 : Right Triangles

Which is the greater quantity?

(a) The hypotenuse of a $45^{\circ}-45^{\circ}-90^{\circ}$ right triangle with a leg of length 20

(b) The hypotenuse of a right triangle with legs of length 19 and 21

Possible Answers:

(a) and (b) are equal

It is impossible to tell from the information given

(a) is greater

(b) is greater

Correct answer:

(b) is greater

Explanation:

The hypotenuses of the triangles measure as follows:

(a) $c = \sqrt {20^{2} + 20^{2} } = \sqrt {400 + 400 } = \sqrt {800}$

(b) $c = \sqrt {19^{2} + 21^{2} } = \sqrt {361 + 441} = \sqrt {802}$

800 < 802 , so $\sqrt {800} < \sqrt {802}$ , making (b) the greater quantity

Report an Error

Example Question #3 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Which is the greater quantity?

(a) The hypotenuse of a right triangle with legs and .

(b) The hypotenuse of a right triangle with legs and .

Possible Answers:

(b) is greater.

(a) and (b) are equal.

It is impossible to tell from the information given.

(a) is greater.

Correct answer:

(a) is greater.

Explanation:

The hypotenuses of the triangles measure as follows:

(a) $c = \sqrt {10^{2} + 15^{2} } = \sqrt {100 + 225 } = \sqrt {325}$

(b) $c = \sqrt {12^{2} + 13^{2} } = \sqrt {144 + 169 } = \sqrt {313}$

325 > 313 , so $\sqrt {325} > \sqrt {313}$ , making (a) the greater quantity.

Report an Error

Example Question #4 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

A right triangle has a leg $4 \frac{1}{2}$ feet long and a hypotenuse $7 \frac{1}{2}$ feet long. Which is the greater quantity?

(a) The length of the second leg of the triangle

(b) 60 inches

Possible Answers:

It is impossible to tell from the information given.

(a) is greater.

(a) and (b) are equal.

(b) is greater.

Correct answer:

(a) is greater.

Explanation:

The length of the second leg can be calculated using the Pythagorean Theorem. Set $c = 7 \frac{1}{2} = \frac{15}{2} , a =4 \frac{1}{2} = \frac{9}{2}$ :

$b ^{2} = c ^{2}-a ^{2}$

$b ^{2} = \left ( \frac{15}{2} \right ) ^{2}- \left ( \frac{9}{2} \right )^{2}\textup{}$

$b ^{2} = \frac{225}{4} -\frac{81}{4}$

$b ^{2} = \frac{144}{4}$

$b ^{2} = 36$

$b = \sqrt{36} = 6$

The second leg therefore measures $6 \times 12 = 72$ inches.

Report an Error

Example Question #5 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

What is the hypotenuse of a right triangle with sides 9 inches and 12 inches?

Possible Answers:

25in

10.5in

27in

225in

15 in

Correct answer:

15 in

Explanation:

Since we're dealing with right triangles, we can use the Pythagorean Theorem ( a^2+b^2=c^2 ). In this formula, a and b are the sides, while c is the hypotenuse. The hypotenuse of a right triangle is the longest side and the side that is opposite the right angle. Now, we can plug into our formula, which looks like this: 9^2+12^2=c^2. We simplify and get 225=c^2 . At this point, isolate c. This means taking the square root of both sides so that your answer is 15in.

Report an Error

Example Question #6 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Right_triangle

The perimeter of a regular pentagon is 75% of that of the triangle in the above diagram. Which is the greater quantity?

(A) The length of one side of the pentagon

(B) One and one-half feet

Possible Answers:

(A) is greater

(B) is greater

It is impossible to determine which is greater from the information given

(A) and (B) are equal

Correct answer:

(B) is greater

Explanation:

By the Pythagorean Theorem, the hypotenuse of the right triangle is

$\sqrt{14^{2}+48^{2}} = \sqrt{196+2,304} = \sqrt{2,500} = 50$ inches, making its perimeter

14 + 48 + 50 =112 inches.

The pentagon in question has sides of length 75% of 112, or

$112 \times 0.75 = 84$ .

Since a pentagon has five sides of equal length, each side will have measure

$84 \div 5 = 16 \frac{4}{5}$ inches.

One and a half feet are equivalent to $12 \times 1 \frac{1}{2} = 18$ inches, so (B) is the greater quantity.

Report an Error

Example Question #7 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Right_triangle

The track at Gauss High School is unusual in that it is shaped like a right triangle, as shown above.

Cary decides to get some exercise by running from point A to point B, then running half of the distance from point B to point C.

Which is the greater quantity?

(A) The distance Cary runs

(B) One-fourth of a mile

Possible Answers:

(A) and (B) are equal

(B) is greater

(A) is greater

It is impossible to determine which is greater from the information given

Correct answer:

(B) is greater

Explanation:

By the Pythagorean Theorem, the distance from B to C is

$\sqrt{600^{2} + 800^{2} }$

$= \sqrt{360,000 + 640,000 }$

$= \sqrt{1,000,000} = 1,000$ feet

Cary runs

$800 + \frac{1}{2} \times1,000 = 800 + 500 = 1,300$ feet

Since 5,280 feet make a mile, one-fourth of a mile is equal to

$5,280 \div 4 = 1,320$ feet.

(B) is greater

Report an Error

Example Question #8 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Right_triangle

Give the length of the hypotenuse of the above right triangle in terms of .

Possible Answers:

$2k ^{2} +8k$

$\sqrt{2k ^{2} +8}$

$\sqrt{2k ^{2} +8k}$

$2 \sqrt{2k}$

$2k ^{2} +8$

Correct answer:

$\sqrt{2k ^{2} +8}$

Explanation:

If we let be the length of the hypotenuse, then by the Pythagorean theorem,

$c = \sqrt{(k+2)^{2}+(k-2)^{2}}$

$c = \sqrt{(k ^{2}+4k+4) +(k ^{2}-4k+4)}$

$c = \sqrt{2k ^{2} +8}$

Report an Error

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

All ISEE Upper Level Quantitative Resources

8 Diagnostic Tests 234 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Denver, French Tutors in Boston, Math Tutors in Houston, Chemistry Tutors in Seattle, Calculus Tutors in Atlanta, Calculus Tutors in Seattle, Reading Tutors in Chicago, SSAT Tutors in Washington DC, English Tutors in Chicago, MCAT Tutors in Seattle

Popular Courses & Classes

MCAT Courses & Classes in New York City, GRE Courses & Classes in San Diego, MCAT Courses & Classes in Boston, LSAT Courses & Classes in Phoenix, ACT Courses & Classes in Chicago, MCAT Courses & Classes in Atlanta, SSAT Courses & Classes in Houston, GMAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Seattle, GMAT Courses & Classes in Houston

Popular Test Prep

LSAT Test Prep in Atlanta, ACT Test Prep in Chicago, ISEE Test Prep in Chicago, LSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Atlanta, GMAT Test Prep in Boston, ACT Test Prep in Denver, GMAT Test Prep in Washington DC, LSAT Test Prep in Los Angeles, SAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Quantitative : ISEE Upper Level (grades 9-12) Quantitative Reasoning

Study concepts, example questions & explanations for ISEE Upper Level Quantitative

All ISEE Upper Level Quantitative Resources

Example Questions

Example Question #1 : How To Find The Area Of An Equilateral Triangle

Example Question #2 : Equilateral Triangles

Example Question #1 : Right Triangles

Example Question #2 : Right Triangles

Example Question #3 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #4 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #5 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #6 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #7 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #8 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

All ISEE Upper Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: