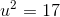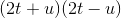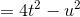ISEE Upper Level Quantitative : Algebraic Concepts
Study concepts, example questions & explanations for ISEE Upper Level Quantitative
All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #15 : How To Multiply Variables
Factor:
We can rewrite as follows:
so the original polynomial is equal to
This is the difference of squares, so it can be factored as
Example Question #16 : How To Multiply Variables
If m is a negative integer, which of the following is an expression that also represents a positive integer?
The easiest way to solve this problem is to take a negative integer to use for m.
For example, 
Plugging in 
This simplifies to
Given that 24 is a positive number, 
Example Question #11 : Variables
When evaluating the expression
assuming you know the values of all five variables, what is the last operation that must be performed?
Multiplication
Cubing
Division
Subtraction
Addition
Addition
By the order of operations, all operations within grouping symbols must be performed first, with the innermost symbols taking precedence. Therefore, the three operations within the brackets - the subtraction, the division, and the cubing - must be performed before the remaining two.
Once these three operations are completed, there remain two more, a division and an addition. Division has precendence in the order of operations, so the last operation performed is the addition.
Example Question #12 : Variables
Which is the greater quantity?
(a) The number of miles in 100 kilometers
(b) The number of kilometers in 100 miles
Note: You may use the conversion factor 1 mile = 1.609 kilometers.
(a) and (b) are equal
(a) is the greater quantity
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(b) is the greater quantity
Since 1 mile is equivalent to 1.609 kilometers, the number of kilometers equivalent to 100 miles can be found by multiplying 100 by 1.609. Conversely, the number of miles equivalent to 100 kilometers can be found by dividing 100 by 1.609.
You do not have to do the actual math to answer the question. Since the conversion factor is greater than one, multiplying any positive number by this factor yields a result greater than dividing that same number by it. Therefore,
and the number of kilometers equivalent to 100 miles, (b), is the greater quantity.
Example Question #13 : Variables
(a) The number of inches in 
(b) The number of ounces in 
(b) is the greater quantity
(a) and (b) are equal
(a) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
One foot comprises twelve inches, so multiply the number of feet by conversion factor 12:
One pound comprises sixteen ounces, so multiply the number of ounces by conversion factor 16:
The two quantities are both equal to 
Example Question #14 : Variables
Which is the greater quantity?
(a) The number of inches in 
(b) The number of days in 
(b) is the greater quantity
(a) is the greater quantity
(a) and (b) are equal
It is impossible to determine which is greater from the information given
(b) is the greater quantity
One yard comprises thirty-six inches, so multiply the number of yards by conversion factor 36:
One week comprises seven days, so multiply the number of weeks by conversion factor 7:
(b) is the greater quantity, since, if 
Example Question #861 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
Evaluate 
Example Question #1 : How To Divide Variables
The ratio of 10 to 14 is closest to what value?
0.04
0.24
0.71
0.57
0.71
Another way to express ratios is through division. 10 divided by 14 is approximate 0.71.
Example Question #1 : How To Divide Variables
If 
A quotient is the result of division. If 
Example Question #2 : How To Divide Variables
(A)
(B)
(A) is greater
(A) and (B) are equal
It is impossible to tell which is greater from the information given
(B) is greater
(B) is greater
Since the quotient of negative numbers is positive, both results will be positive.
We can rewrite both of these as products of positive numbers, as follows:
making (B) greater.
Certified Tutor
Certified Tutor
All ISEE Upper Level Quantitative Resources
