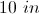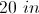ISEE Upper Level Math : Geometry
Study concepts, example questions & explanations for ISEE Upper Level Math
All ISEE Upper Level Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Side Of A Rectangle
The area of a rectangle is 100 square inches. What is the width of the rectangle?
Cannot be determined
Cannot be determined
Without more information we cannot determine the width of a rectangle based on its area alone.
If we know this is a square and therefore that all sides are equal, we could simply take the square root of 100, which is 10.
However, we do not know that all sides are equal. We need to know the length of the rectangle to solve this problem. Therefore the best we can do is see what the equation would look like if we knew the length.
or
where 
Note: the incorrect answer choices are all factors of 100 and possible answers, but we can't be sure which, if any, are the right one.
Example Question #2 : How To Find The Length Of The Side Of A Rectangle
The area of a rectangle is 40; its width is 
Let 
Example Question #1 : How To Find The Length Of The Side Of A Rectangle
The perimeter of a rectangle is 70; its width is 
Let 
Replace 
Example Question #1 : How To Find The Length Of The Side Of A Rectangle
A rectangle has perimeter 56. Its length is 
Insufficient information is given to answer the question.
Substitute 
Example Question #312 : Geometry
You have a shed that you use for storing your gardening supplies and outdoor tools. If the shed has a footprint of 
You have a shed that you use for storing your gardening supplies and outdoor tools. If the shed has a footprint of 
We are given a rectangle with a known area and width, and asked to find the length.
To do so, recall this formula:
We know A and w, so simply work backwards to solve for l
So, our answer is 17.75 ft
Example Question #1 : How To Find The Surface Area Of A Prism
Find the surface area of a non-cubic prism with the following measurements:
The surface area of a non-cubic prism can be determined using the equation:
Example Question #2 : Solid Geometry
The above diagram shows a rectangular solid. The shaded side is a square. In terms of 
A square has four sides of equal length, as seen in the diagram below.
All six sides are rectangles, so their areas are equal to the products of their dimensions:
Top, bottom, front, back (four surfaces):
Left, right (two surfaces):
The total surface area:
Example Question #1 : Finding Volume Of A Rectangular Prism
A rectangular prism has a width of 3 inches, a length of 6 inches, and a height triple its length. Find the volume of the prism.
A rectangular prism has a width of 3 inches, a length of 6 inches, and a height triple its length. Find the volume of the prism.
Find the volume of a rectangular prism via the following:
Where l, w, and h are the length width and height, respectively.
We know our length and width, and we are told that our height is triple the length, so...
Now that we have all our measurements, plug them in and solve:
Example Question #1 : Finding Volume Of A Rectangular Prism
The above diagram shows a rectangular solid. The shaded side is a square. In terms of 
A square has four sides of equal length, as seen in the diagram below.
The volume of the solid is equal to the product of its length, width, and height, as follows:
Example Question #1 : Pyramids
A pyramid has height 4 feet. Its base is a square with sidelength 3 feet. Give its volume in cubic inches.
Convert each measurement from inches to feet by multiplying it by 12:
Height: 4 feet = 
Sidelength of the base: 3 feet = 
The volume of a pyramid is
Since the base is a square, we can replace 
Substitute
The pyramid has volume 20,736 cubic inches.
Certified Tutor
All ISEE Upper Level Math Resources
