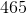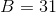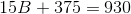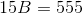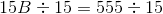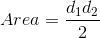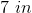Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : Geometry

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Area Of A Trapezoid

A trapezoid has the base lengths of and . The area of the trapezoid is 8t^2 . Give the height of the trapezoid in terms of .

Possible Answers:

Correct answer:

Explanation:

The area of a trapezoid is given by

$Area=(\frac{b_{1}+b_{2}}{2})h$ ,

where $b_{}1$ , $b_{}2$ are the lengths of each base and is the altitude (height) of the trapezoid.

$Area=(\frac{b_{1}+b_{2}}{2})h=(\frac{3t+t}{2})\times h=8t^2\Rightarrow (2t)h=8t^2$

$\Rightarrow h=\frac{8t^2}{2t}=4t$

Report an Error

Example Question #3 : How To Find The Area Of A Trapezoid

In the following trapezoid b=2a and a=h . The area of the trapezoid is 54 square inches. Give the height of the trapezoid. Figure not drawn to scale.

Trap

Possible Answers:

$4\ in$

$5\ in$

$7\ in$

$3\ in$

$6\ in$

Correct answer:

$6\ in$

Explanation:

The area of a trapezoid is given by

$Area=(\frac{b_{1}+b_{2}}{2})h$ ,

where $b_{}1$ , $b_{}2$ are the lengths of each base and is the altitude (height) of the trapezoid.

$b_{1}=a$

$b_{2}=b=2a$

h=a

Substitute these values into the area formula:

$Area=(\frac{b_{1}+b_{2}}{2})h=(\frac{a+2a}{2})a=54\Rightarrow \frac{3a^2}{2}=54\Rightarrow a^2=36\Rightarrow a=6\ in$

Report an Error

Example Question #4 : How To Find The Area Of A Trapezoid

Square 3

What is the area of the shaded portion of the above square?

Possible Answers:

401

408

492

551

Correct answer:

492

Explanation:

Quadrilateral SQUR - the shaded region - is a trapezoid with bases $\overline{SR}$ and $\overline{QU }$ , and altitude $\overline{SQ}$ . The area of the trapezoid can be calculated using the formula

$A = \frac{1}{2} ( b_{1}+ b_{2} ) h$ ,

where $b_{1} = SR = 24$ and $b_{2} = QU$ , and h = SQ = 25 .

The length of $\overline{UA}$ can be found by setting c = 25 and b = 24 and applying the Pythagorean Theorem:

$a = \sqrt{c^{2} - b^{2}} = \sqrt{25^{2} - 24^{2}} =\sqrt{625- 576} = \sqrt{49} = 7$

Therefore,

QU = QA - UA = 24 - 7 = 17 .

Substituting:

$A = \frac{1}{2} ( b_{1}+ b_{2} ) h$

$A = \frac{1}{2} ( 24 + 17) 24$

$A = \frac{1}{2} \cdot 41 \cdot 24$

A = 492

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Trapezoid

Trapezoid

Note: Figure NOT drawn to scale.

The area of the above trapezoid is 465 . What is ?

Possible Answers:

B = 31

B = 47

B = 37

B = 42

B = 35

Correct answer:

B = 37

Explanation:

Substitute A = 465, b = 25, h = 15 into the formula for the area of a trapezoid:

$\frac{1}{2} (B + b)h = A$

$\frac{1}{2} (B + 25) \cdot 15 = 465$

$2 \cdot \frac{1}{2} (B + 25) \cdot 15 = 2 \cdot 465$

$(B + 25) \cdot 15 = 930$

15 B + 375 = 930

15 B + 375 - 375 = 930 - 375

15 B = 555

$15 B \div 15 = 555\div 15$

B = 37

Report an Error

Example Question #1 : How To Find The Area Of A Kite

Cassie is making a kite for her little brother. She has two plastic tubes to use as the skeleton, measuring inches and inches. If these two tubes represent the diagnals of the kite, how many square inches of paper will she need to make the kite?

Possible Answers:

Correct answer:

Explanation:

To find the area of a kite, use the formula $\frac{1}{2}ab$ , where represents one diagnal and represents the other.

Since Cassie has one tube measuring inches, we can substitute for . We can also substitute the other tube that measures inches in for .

$\frac{1}{2}(7)(12)=42\ in^{2}$

Report an Error

Example Question #271 : Plane Geometry

Two diagonals of a kite have the lengths of $10\ in$ and $6\ in$ . Give the area of the kite.

Possible Answers:

$45\ in^2$

$36\ in^2$

$30\ in^2$

$80\ in^2$

$60\ in^2$

Correct answer:

$30\ in^2$

Explanation:

The area of a kite is half the product of the diagonals, i.e.

$Area=\frac{d_{1}d_{2}}{2}$ ,

where $d_{1}$ and $d_{2}$ are the lengths of the diagonals.

$Area=\frac{d_{1}d_{2}}{2}=\frac{6\times 10}{2}=30\ in^2$

Report an Error

Example Question #272 : Geometry

In the following kite, $a=10\ cm$ , $b=15\ cm$ and $\angle C=120^{\circ}$ . Give the area of the kite. Figure not drawn to scale.

Kite

Possible Answers:

$150\sqrt{3}\ cm^2$

$150\ cm^2$

$75\sqrt{3}\ cm^2$

$75\sqrt{2}\ cm^2$

$75\ cm^2$

Correct answer:

$75\sqrt{3}\ cm^2$

Explanation:

When you know the length of two unequal sides of a kite and their included angle, the following formula can be used to find the area of a kite:

$Area=ab\times sinC$ ,

where are the lengths of two unequal sides, is the angle between them and sin is the sine function.

$Area=ab\times sinC=10\times 15\times sin120^{\circ}=10\times 15\times \frac{\sqrt{3}}{2}\Rightarrow Area=75\sqrt{3}\ cm^2$

Report an Error

Example Question #2 : Kites

Find the area of a kite with one diagonal having length 18in and the other diagonal having a length that is half the first diagonal.

Possible Answers:

$54\text{in}^2$

$162\text{in}^2$

$76\text{in}^2$

$108\text{in}^2$

$81\text{in}^2$

Correct answer:

$81\text{in}^2$

Explanation:

To find the area of a kite, we will use the following formula:

$A = \frac{pq}{2}$

where p and q are the lengths of the diagonals of the kite.

Now, we know the length of one diagonal is 18in. We also know the other diagonal is half of the first diagonal. Therefore, the second diagonal has a length of 9in.

Knowing this, we can substitute into the formula. We get

$A = \frac{18\text{in} \cdot 9\text{in}}{2}$

$A = \frac{162\text{in}^2}{2}$

$A = 81\text{in}^2$

Report an Error

Example Question #1 : Kites

A kite has the area of $60\ in^2$ . One of the diagonals of the kite has length $15\ in$ . Give the length of the other diagonal of the kite.

Possible Answers:

$4\ in$

$8\ in$

$6\ in$

$7\ in$

$5\ in$

Correct answer:

$8\ in$

Explanation:

The area of a kite is half the product of the diagonals, i.e.

$Area=\frac{d_{1}d_{2}}{2}$ ,

where $d_{1}$ and $d_{2}$ are the lengths of the diagonals.

$Area=\frac{d_{1}d_{2}}{2}=\frac{{15}\times {d_{2}}}{2}=60\Rightarrow d_{2}=\frac{60\times 2}{15}\Rightarrow d_{2}=8\ in$

Report an Error

Example Question #1 : How To Find The Area Of A Parallelogram

Parallelogram2

Give the area of the above parallelogram if BC = 10 .

Possible Answers:

$25\sqrt{3}$

$50\sqrt{2}$

$25\sqrt{2}$

Correct answer:

$25\sqrt{3}$

Explanation:

Multiply height by base to get the area.

By the 30-60-90 Theorem:

$BD = \frac{BC}{2} = \frac{10}{2}} = 5$

and

$CD =BD \cdot \sqrt{3} = 5\sqrt{3}$

The area is therefore

$BD \cdot CD = 5 \cdot 5\sqrt{3} = 25\sqrt{3}$

Report an Error

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View Tutors

Pushpendra
Certified Tutor

university of allahabad, Bachelor of Science, Mathematics.

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Phoenix, ACT Tutors in Houston, Algebra Tutors in Chicago, English Tutors in Los Angeles, ACT Tutors in Philadelphia, Algebra Tutors in Miami, ISEE Tutors in Miami, LSAT Tutors in New York City, Reading Tutors in Los Angeles, Chemistry Tutors in Los Angeles

Popular Courses & Classes

Spanish Courses & Classes in Los Angeles, SSAT Courses & Classes in Denver, Spanish Courses & Classes in Washington DC, MCAT Courses & Classes in Phoenix, ISEE Courses & Classes in Miami, GMAT Courses & Classes in Boston, MCAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Denver, MCAT Courses & Classes in Miami

Popular Test Prep

ISEE Test Prep in Miami, SSAT Test Prep in Houston, LSAT Test Prep in New York City, ISEE Test Prep in Seattle, MCAT Test Prep in Denver, LSAT Test Prep in Boston, SAT Test Prep in Phoenix, GMAT Test Prep in San Diego, ACT Test Prep in Houston, GRE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : Geometry

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #3 : How To Find The Area Of A Trapezoid

Example Question #4 : How To Find The Area Of A Trapezoid

Example Question #1 : How To Find The Length Of The Side Of A Trapezoid

Example Question #1 : How To Find The Area Of A Kite

Example Question #271 : Plane Geometry

Example Question #272 : Geometry

Example Question #2 : Kites

Example Question #1 : Kites

Example Question #1 : How To Find The Area Of A Parallelogram

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: