ISEE Upper Level Math : Data Analysis
Study concepts, example questions & explanations for ISEE Upper Level Math
All ISEE Upper Level Math Resources
Example Questions
Example Question #3 : Tables
Nine students are running for student council; each member of the student body will vote for four. Freida's boyfriend Greg is running and she wants to vote for him. How many ways can she cast a ballot so that she can include Greg among her choices?
Since Freida has already chosen one of the nine candidates, she will choose three of the remaining eight, Since order is unimportant, the number of ways to do this is the number of combinations of three chosen from eight.
Example Question #2 : How To Find The Answer From A Table
The following is a portion of the menu at a coffee shop:
A boss treats her employees to coffee at this coffee shop. She orders three lattes, three Americanos, two espressos, a cappucino, and a Turkish coffee. The tax is 
Add the prices of the ten items:
The price of the beverages after tax is 
The change out of a 
Example Question #1 : How To Find The Answer From A Table
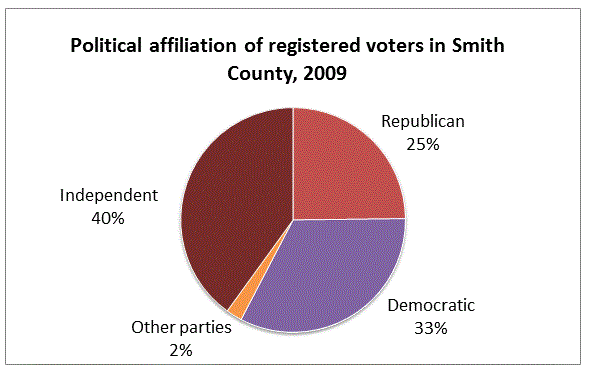
Refer to the above circle graph. There are 
It is impossible to tell from the information given.
Set 
Example Question #561 : Isee Upper Level (Grades 9 12) Mathematics Achievement
The above is an annual income tax table for a given state. Married couples will pay the tax rate for the tax bracket in which their entire income falls.
Mr. Jackson earned $34,287 last year; Mrs. Jackson earned $25,879. How much will the couple pay in income tax for that year (nearest hundred dollars)?
The Jackson's income totaled
This puts them in the 1.7% tax bracket, so they will pay
The correct response is $1,000.
Example Question #4 : Tables
Jefferson Elementary School has seven eighth-grade teachers; each teacher has the number of boys and girls listed above.
How many teachers have classes in which at least 40% of the students are boys?
Five
Four
Six
Seven
Six
Five teachers each have 30 students, and 40% of 30 is
Two teachers each have 29 students, and 40% of 29 is
Therefore, to have a class that is at least 40% boys, a teacher must have 12 boys at minimum. Only Mr. Georghiou does not have at least 12 boys, so the correct response is six.
Example Question #6 : How To Find The Answer From A Table
Adams Elementary School has seven fifth-grade teachers; each teacher has been assigned the number of boys and girls listed above.
However, just before the start of the school year, Mrs. Henry has been hired as an additional fifth-grade teacher. It is desired that some students be reassigned to her class so that each class have the same number of students, or as close to the same number of students as possible. If this is done, how many students will be in Mrs. Henry's class?
This problem is essentially figuring out what will be the average number of students in each class if there are eight teachers instead of seven.
Add the fourteen numbers in the table:
If there are eight teachers, then each teacher, including Mrs. Henry, will have
Example Question #11 : Tables
Washington Elementary School has seven eighth-grade teachers; each teacher has the number of boys and girls listed above.
An eighth-grade girl has transferred from another school. It is desired that no teacher have more than thirty students overall or eighteen girls in his or her class. Of the seven teachers, how many could accept the girl into his or her class?
One
Seven
Six
Two
One
We can eliminate Cermak and Georghiou immediately since each has eighteen girls in his class. Of the other five:
Adams has 
Boyer has 
Donovan has 
Esterhaus has 
Finnegan has 
Only Mrs. Finnegan's class could accept the new girl without going against the wishes of the school. The correct response is one.
Example Question #12 : Tables
A popular word game uses one hundred tiles, each of which is marked with a letter or a blank. The distribution of the tiles is shown above, with each letter paired with the number of tiles marked with that letter. Notice that there are two blank tiles.
What percent of the tiles are marked with consonants?
Note: for purposes of this question, "Y" is a consonant.
Counting the number of tiles with vowels is much easier.
Out of the 100 tiles, there are nine "A" tiles, twelve "E" tiles, nine "I" tiles, eight "O" tiles, and four "U" tiles. This is a total of
tiles out of 100.
There are also two blanks, so the number of tiles marked with consonants is
56 out of 100 is 56%.
Example Question #11 : Tables
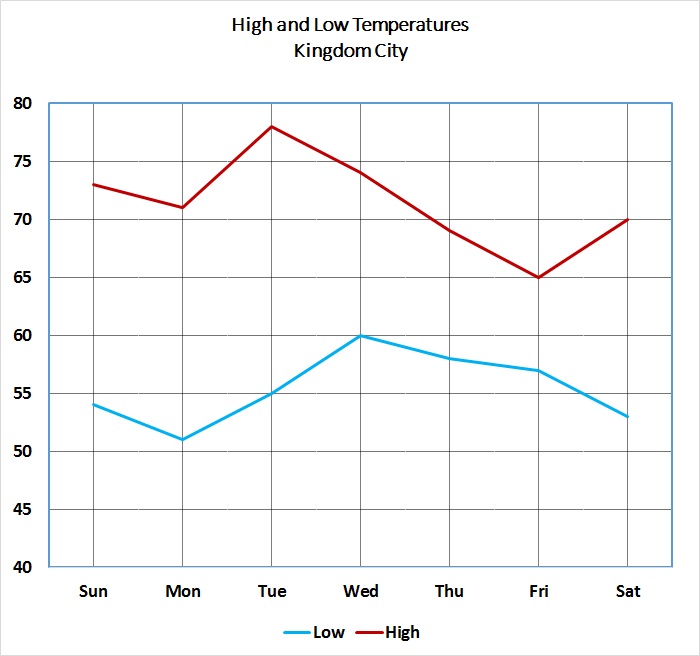
Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period.
Between which two consecutive days did the high temperature show an increase?
Between Tuesday and Wednesday
Between Wednesday and Thursday
Between Monday and Tuesday
Between Thursday and Friday
Between Monday and Tuesday
Examining the high temperature line, it can be seen that, among the four choices given, only the segment connecting Monday to Tuesday has a positive slope (lower left to upper right).
Therefore, of the four choices, Monday to Tuesday is correct.
Example Question #14 : Tables
A popular word game uses one hundred tiles, each of which is marked with a letter or a blank. The distribution of the tiles is shown above, with each letter paired with the number of tiles marked with that letter. Notice that there are two blank tiles.
What percent of the vowel tiles are marked with an "A"? (Nearest whole percent).
Note: for purposes of this question, "Y" is a consonant.
There are nine "A" tiles, twelve "E" tiles, nine "I" tiles, eight "O" tiles, and four "U" tiles. This is a total of
vowel tiles.
Out of these tiles, 9 are marked with an "E"; this is
This rounds to 21%.
All ISEE Upper Level Math Resources
