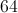All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #1731 : Grade 6
Find the median of this set of numbers:
60, 74, 51, 43, 91,62, 65
First, place the numbers in order from least to greatest:
Then, identify the middle number: 62.
Example Question #1732 : Grade 6
Give the median of the following nine scores:
Arrange the scores from least to greatest.
There are an odd number (nine) of scores, so the median of the scores is the one that falls in the center - namely, 72.
Example Question #1 : Find Median
What is the median of the following set of numbers:
No number is the median for this set of numbers
The median is the number with an equal number of other items both above and below it. There are 9 total numbers in the list, 4 of them are below 7, and 4 of them are above 7.
Example Question #1733 : Grade 6
What is the median of the values 




The median of a set of values is the value that is in the middle when you rearrange the values from least to greatest. In this set, the values can be rearranged as 





Example Question #1 : Find Median
On a math test that the teacher gave her students, the scores were as follows:
What was the median score?
The median is the middle number in a set when the set of numbers is ordered sequentially.
When the intial set is reordered sequentially, you get the bottom set. (The top set is the original ordering of the numbers.)
In this sequential set of 7 numbers, the number 89 is in the fourth posiiton and exactly in the middle. Therefore, it is the mean.
Example Question #6 : How To Find Median
What is the median of this set of numbers?
To find the median of a set of numbers, you must first reorder them from smallest to largest. Below is the set reordered as such:
The median is the middle number of the set. Here, 57 is the middle number. Therefore, it is the median and the correct answer.
Example Question #11 : How To Find Median
Given the following data sets of data, identify how the median would change if an additional data point of 
Data Set:
New Data Set:
First, we need to find the median for the first data set:
We must put the numbers in order from least to greatest:
Since there is an even number of items in the data set, we will take the average of the middle two numbers to find the median.
The median for this data set is:

Next, we must find the new median for the new data set:
Again, we must put the numbers in order from least to greatest:
Since there is an odd number of items, we can choose the middle number to be the median.
In this case, the middle number is 
Therefore, we know that the median will decrease by 
Example Question #11 : Median
Horatio's soccer team has scored the below number of goals in their last eight games, what is the median number of goals that have been scored?
First we must put the numbers 
After the numbers are in order, if it is an odd number of numbers we chose the middle number - that is the median.
In this case, we have an even number of numbers, so we must take the average of the middle two numbers which is given below:
So the median is 
Example Question #1741 : Grade 6
Horatio's soccer team has scored the below number of goals in their last 
Horatio calculates the median to be 



The median will remain unchanged
The median will increase by
The median will increase by
The median will increase by
The median will remain unchanged
When finding the median we must first reorganize the numbers from least to greatest, here is what the numbers are before and after they were organized.
Given:
After Organized from least to greatest:
In order to find the Median for an even number of numbers (we have 
Here we would add 


If we were to change the 




The middle two numbers are still 

The Median will remain unchanged.
Example Question #15 : Find Median
Find the median of the data set provided:

In order to answer this question correctly, we need to recall the definition of median:
Median: The median of a data set is the middle value, when the data set is ordered from least to greatest.
In order to find the median, we need to first organize the data from least to greatest:
Next, we can solve for the median by finding the middlemost number in our data:
The median for this data set is
Certified Tutor
All ISEE Middle Level Quantitative Resources