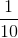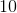To find the probability of an event, we will use the following formula:

So, given the event of drawing a 3 from a deck of cards, we can calculate the following:

Beause there are four 3s we could draw from a deck of cards

•          3 of hearts
•          3 of diamonds
•          3 of clubs
•          3 of spades

Now we can calculate the following:

Because there are 52 cards in the deck we could potentially draw.

Knowing this, we can substitute into the formula.  We get

To find the probability of an event, we will use the following formula:

Now, given the event of grabbing  a green crayon from the bag, we can calculate the following:

Because there are 4 green crayons in the bag.

We can also calculate the following:

Because there are 24 total crayons we could potentially grab from the bag.

Knowing all of this, we can substitute into the formula.  We get

Therefore, the probability of grabbing a green crayon is .

To find the probability of an event, we will use the following formula:

Now, given the event of calling on a girl, we can determine:

because there are 24 girls in the class the teacher could call on.

We can determine:

because there are 56 total students in the class the teacher could potentially call on:

• 24 girls
• 32 boys

Now, we can substitute into the formula.  We get

Therefore, the probability the teacher calls on a girl is .

To find the probability of an event, we will use the following formula:

So, given the event of drawing a 7 from a deck of cards we can calculate the following:

because there are four ways we can draw a 7 from the deck: 

• 7 of clubs
• 7 of spades
• 7 of hearts
• 7 of diamonds

Now, we can calculate the following:

because there are 52 cards we could potentially draw from a deck of cards.

Knowing this, we can substitute into the formula.  We get

Therefore, the probability of drawing a 7 from a deck of cards is .

To find the probability of an event, we will use the following formula:

So, given the event of drawing heart, we can calculate the following:

because there are 13 ways we can draw a heart:

• Ace
• Two
• Three
• Four
• Five
• Six
• Seven
• Eight
• Nine
• Ten
• Jack
• Queen
• King

Now, we can calculate the following:

because there are 52 cards we could potentially draw from a deck of cards.

Knowing this, we can substitute into the formula.  We get

Therefore, the probability of drawing a heart from a deck of cards is .

To find the probability of an event, we will use the following formula:

Now, given the event of grabbing a red crayon from the box, we can calculate:

because there are 4 red crayons in the box we could grab.

We can also calculate:

because there are 17 total crayons we could potentially grab:

• 9 blue crayons
• 3 green crayons
• 4 red crayons
• 1 yellow crayon

So, we get

Therefore, the probability of grabbing a red crayon from the box is .

To find the probability of an event, we will use the following formula:

So, given the event of drawing a 5, we can calculate the following:

because there are 4 ways we can draw a 5 from a deck:

•          5 of clubs
•          5 of spades
•          5 of hearts
•          5 of diamonds

Now, we can calculate the following:

because there are 52 cards we could potentially draw from a deck of cards.

Knowing this, we can substitute into the formula.  We get

Therefore, the probability of drawing a 5 from a deck of cards is .

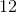
To find the probability of an event, we will use the following formula:

Now, in the event of calling on a boy in the class, we can determine the number of ways the event can happen:

because there are 10 boy students in the class.

To find the number of possible outcomes, we get

because there are 22 total students the teacher could potentially call on.

Knowing all of this, we can substitute into the formula.  We get

Reduce:

Therefore, the probability of calling on a boy is .

To find the probability of an event, you divide the possible outcomes of that event by total outcomes.  

The event outcomes would be the  seniors on the bus.  

The total outcomes is the number of students on the bus which is 

.  

So the probability of picking a senior would be 

.

To find the probability of an event, we will use the following formula:

Now, we will first determine the number of ways the event can happen. So, given the event of rolling a factor of 6, we get

because there are 4 different factors of 6 that we can roll:

• 1
• 2
• 3
• 6

Now, we will determine the total number of possible events.  So,

because there are 6 different numbers we can roll:

• 1
• 2
• 3
• 4
• 5
• 6

Knowing this, we will substitute into the formula.  We get

Now, we will simplify.  We get

Therefore, the probability of rolling a factor of 6 is .