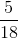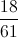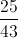To find the probability of an event, we use the following:

So, when looking at the event of drawing a 2 from a deck of cards, we get

It is 4 because we can draw a 2 from a deck of cards 4 different ways:

• 2 of hearts
• 2 of diamonds
• 2 of clubs
• 2 of spades

Now, 

because there are 52 cards in the entire deck.  Now,

We can simplify, we get

Therefore, the probability of drawing a 2 from a deck of cards is 

To find the probability of an event, we use the following:

So, when looking at the event of drawing a 9 of hearts from a deck of cards, we get

It is 1 because we can draw a 9 of hearts from a deck of cards in only 1 way:

• 9 of hearts

Now, 

because there are 52 cards in the entire deck.  Now,

Therefore, the probability of drawing a 2 from a deck of cards is 

Given that  of the class is girls, and there are  students, we must first determine how many girls are in the class. 

Because  is double the value of ,  is double the value of .  should be half of .

If  of the  girls wear skirts, then we can subtract to find the number of girls not wearing skirts.

The pizza that Billy's mom baked was composed of these types of slices:

Half the slices have pepperoni only. Two of the slices have both pepperoni and onoins. One slice has onions only. One slice has only cheese. 

Therefore, 

 slices had pepperoni because 

 slices had pepperoni and onions 

 slice had onion only

 slice had only cheese. 

Billy could eat either the onion only slice, or the cheese only slice. This means that out of  pieces of pizza, he could eat . 

Given that  is the percent equivalent of , that is the correct answer. 

The following rolls result in the difference of the dice being :

 and the reverse of each of these.

These are  rolls out of a possible , so the probability of this event is 

The rolls that yield a product between  and  inclusive are:

Therefore there are  rolls that fit our criteria out of a total of  possible rolls, so the probability of this outcome is .

The probability of an event based on observation (empirical probability) can be calculated by dividing the number of times the event occurs by the number of trials total. Since there were  trials and  heads, there were  tails.

The probability of tails is therefore given by the number of tails divided by the total number of trials. Both terms are divisible by , allowing us to simplify the fraction.

There are   possible rolls of two fair six-sided dice, each of which will come up with equal probability. The set of rolls is shown below, with the ways to roll a sum of 8 or 9 indicated.

There are 9 ways out of 36 to roll a sum of 8 or 9, making the probability of this outcome .

To find the probability of an event, we will use the following formula:

So, if we look at the event of drawing a 10 from a deck of cards, we can determine the following:

because there are 4 ways we can draw a 10:

• 10 of hearts
• 10 of diamonds
• 10 of clubs
• 10 of spades

because there are 52 total cards to choose from.  

Knowing all of this, we can substitute into the formula.  We get

Now, we simplify.

Therefore, the probability of drawing a 10 from a deck of cards is .

The first step is to take the seniors out of the equation 

.  

With  students left over, you divide that number by three since each of the three remaining groups are equally likely.  

This gives you a final answer of .