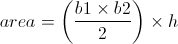Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : ISEE Lower Level (grades 5-6) Quantitative Reasoning

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #221 : Geometry

Square ABCD has coordinate points: A(0,0) , B(5,0) , C(5,5) , D(0,5) . Find the area of square ABCD .

Possible Answers:

square units

Correct answer:

square units

Explanation:

The fomula used to find the area of a square is s^2.

To find the side length of our square look at the distance between the x or y values two of our coordinate points.

A=(0,0), B=(5,0) thus the length of a side is 5 units.

Thus, the correct answer is:

A=s^2
$A=5^2=5\times 5=25$

Report an Error

Example Question #1 : How To Find A Square On A Coordinate Plane

Square ABCD has coordinate points: A(0,0) , B(5,0) , C(5,5) , D(0,5) . Find the perimeter of square ABCD .

Possible Answers:

Correct answer:

Explanation:

The perimeter of square ABCD can be found by applying the formula:

, where the length of one side of the square.

To find the length of the square look at the coordinates:

$A=(0,0), B=(5,0)\rightarrow S=5$

Thus,
S=5
$p=4\times5=20$

Report an Error

Example Question #2 : How To Find A Square On A Coordinate Plane

The points with coordinates (7, 5), (5, 3), (5, 5), (7, 3) are the vertices of which kind of quadrilateral?

Possible Answers:

Trapezoid

Square

Kite

Parallelogram

Correct answer:

Square

Explanation:

If the points are plotted on to a graph, you should notice that the points form a square with side lengths of .

Report an Error

Example Question #1 : Quadrilaterals

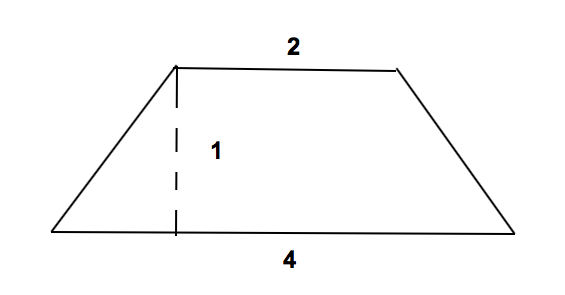
Trapezoid3

What is the area of a trapezoid if its height is 1, its long base is 4, and its short base is 2?

Possible Answers:

8.5

Correct answer:

Explanation:

The area of a trapezoid is given by the formula $\frac{1}{2} *height* (base_{long} + base_{short})$ .

We know that the height is 1, the long base is 4, and the short base is 2.

$\frac{1}{2} *height* (base_{long} + base_{short})=\frac{1}{2} *(1)* ((4) + (2))$

$\frac{1}{2}*(6)$

Report an Error

Example Question #1 : How To Find The Area Of A Trapezoid

Which formula would you use to find the area of a trapezoid?

Possible Answers:

$area=\left ( \frac{b1+b2}{2} \right )\times h$

$area=\left ( \frac{b1+b2}{h} \right )\times 2$

$area=\left ( \frac{b1\times b2}{2} \right )\times h$

$area=\left ( \frac{h}{2} \right )\times b1+b2$

Correct answer:

$area=\left ( \frac{b1+b2}{2} \right )\times h$

Explanation:

The find the area of a trapezoid, use:

$area=\left ( \frac{b1+b2}{2} \right )\times h$

Report an Error

Example Question #2 : Quadrilaterals

Yard

The above diagram shows a trapezoidal home within a rectangular yard. What is the area of the yard?

Possible Answers:

$11,350 \textrm{ m}^{2}$

$8,925 \textrm{ m}^{2}$

$7,525 \textrm{ m}^{2}$

$6,125 \textrm{ m}^{2}$

$10,325 \textrm{ m}^{2}$

Correct answer:

$7,525 \textrm{ m}^{2}$

Explanation:

The area of the yard is the area of the small trapezoid subtracted from that of the large rectangle. The area of a rectangle is the product of its length and its height, so the large rectangle has area

$105 \times 85 = 8,925$ square meters.

The area of a trapezoid is half the product of its height and the sum of its two parallel sides (bases), so the small trapezoid has area

$\frac{1}{2} \times 40 \times (30 + 40) = \frac{1}{2} \times 40 \times 70 = 1,400$ square meters.

The area of the yard is the difference of the two:

8,925- 1,400 = 7,525 square meters.

Report an Error

Example Question #1 : Plane Geometry

Yard

Note: Figure NOT drawn to scale.

Mr. Smith owns the triangular piece of land seen in the above diagram. He sells the trapezoidal parcel shown at bottom right to his brother. What is the area of the land he retains?

Possible Answers:

$41,000 \textrm{ ft}^{2}$

$46,500 \textrm{ ft}^{2}$

$16,000 \textrm{ ft}^{2}$

$20,500\textrm{ ft}^{2}$

$35,600 \textrm{ ft}^{2}$

Correct answer:

$20,500\textrm{ ft}^{2}$

Explanation:

The area of a triangle is half the product of its base and its height, so Mr. Smith's parcel originally had area

$\frac{1}{2 } \times 200 \times 250 = 25,000$ square feet.

The area of a trapezoid is the half product of its height and the sum of its two parallel sides (bases), so the portion Mr. Smith sold to his brother has area

$\frac{1}{2} \times 50 \times (80 + 100) = 4,500$ square feet.

Therefore, Mr. Smith retains a parcel of area

25,000 - 4,500 = 20,500 square feet.

Report an Error

Example Question #1 : Plane Geometry

Screenshot_2015-03-29_at_3.04.28_pm

What is the area of the above trapezoid?

Possible Answers:

$40\:in^2$

$45\:in^2$

$63\:in^2$

$35\:in^2$

$52\:in^2$

Correct answer:

$40\:in^2$

Explanation:

The formula for the area of a trapezoid is $\frac{base_1 + base_2}{2}\cdot height$

In other words, find the average of the bases and multiply by the height. Substituting in the values of the bases for the given trapezoid, and , you get:

$\frac{9\:in+7\:in}{2}\cdot 5\:in = 8\:in\cdot 5\:in=40\:in^2$

Report an Error

Example Question #1 : Quadrilaterals

Screenshot_2015-03-29_at_3.18.30_pm

What is the area of the above trapezoid?

Possible Answers:

$40\:cm^2$

$50\:cm^2$

$96\:cm^2$

$35\:cm^2$

$60\:cm^2$

Correct answer:

$50\:cm^2$

Explanation:

The formula for the area of a trapezoid is $\frac{base_1 + base_2}{2}\cdot height$

In other words, find the average of the bases and multiply by the height. Substituting the values of the bases of the given trapezoid, $8\:cm$ and $12\:cm$ , into the equation, you get:

$\frac{8\:cm+12\:cm}{2}\cdot 5\:cm = 10\:cm\cdot 5\:cm=50\:cm^2$

The area of the trapezoid is thus $50\:cm^2$ .

Report an Error

Example Question #981 : Isee Lower Level (Grades 5 6) Quantitative Reasoning

Find the perimeter of the following trapezoid.

Possible Answers:

Correct answer:

Explanation:

In order to find the perimeter of the trapezoid, we have to add up all the outer sides:

6+3+5+7=21

Report an Error

View Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Giovanna
Certified Tutor

PROVIDENCE College, Bachelor of Science, Accounting and Business Management. University of Rhode Island, Master of Arts Teac...

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Denver, Calculus Tutors in San Diego, LSAT Tutors in Boston, LSAT Tutors in Los Angeles, SAT Tutors in Chicago, ISEE Tutors in Houston, Computer Science Tutors in Atlanta, Biology Tutors in San Francisco-Bay Area, Reading Tutors in Denver, Computer Science Tutors in Dallas Fort Worth

Popular Courses & Classes

Spanish Courses & Classes in Denver, SAT Courses & Classes in Boston, SAT Courses & Classes in Seattle, SSAT Courses & Classes in Chicago, Spanish Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in San Diego, Spanish Courses & Classes in Seattle, GMAT Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, LSAT Courses & Classes in Atlanta

Popular Test Prep

SSAT Test Prep in Seattle, GRE Test Prep in New York City, ISEE Test Prep in Washington DC, ISEE Test Prep in Los Angeles, GMAT Test Prep in Boston, MCAT Test Prep in Seattle, SSAT Test Prep in San Diego, SAT Test Prep in Los Angeles, GMAT Test Prep in Philadelphia, SAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : ISEE Lower Level (grades 5-6) Quantitative Reasoning

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #221 : Geometry

Example Question #1 : How To Find A Square On A Coordinate Plane

Example Question #2 : How To Find A Square On A Coordinate Plane

Example Question #1 : Quadrilaterals

Example Question #1 : How To Find The Area Of A Trapezoid

Example Question #2 : Quadrilaterals

Example Question #1 : Plane Geometry

Example Question #1 : Plane Geometry

Example Question #1 : Quadrilaterals

Example Question #981 : Isee Lower Level (Grades 5 6) Quantitative Reasoning

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: