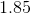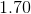All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #1641 : Isee Lower Level (Grades 5 6) Quantitative Reasoning
What is the next number:
In this sequence of numbers, there is an important pattern to recognize. Each number is greater than the number prior to it by a margin of 
Example Question #1642 : Isee Lower Level (Grades 5 6) Quantitative Reasoning
Find the missing number in the list:
In this sequence of numbers, there is an important pattern to recognize. Each number is less than the previous number in the sequence by a difference of 

Example Question #14 : How To Find The Missing Part Of A List
What is the missing number in the following sequence:
In this sequence of numbers, there is an important pattern to recognize. Each number is greater than the number prior to it by a margin of 





Example Question #82 : Data Analysis And Probability
What is the missing value of 
In this sequence, every subsequent number is 




Example Question #1 : Tables
Use the following table to determine the cost of purchasing two books.

The relationship between the values is 
where 

Once we realize this, we can determine how much purchasing two books 
Example Question #2 : Tables
Use the table to determine how much one cupcake would cost.

We can determine the relationship between the values by creating a ratio of number of cupcakes to cost:

Where 
We can now solve for 
The cost of one cupcake is then $0.85
Example Question #3 : Tables
The following table consists of the test grades from 


We were told the grades are from 
We know there is a total of 


So the missing value is eight.
Example Question #1 : Tables
Use the table to determine how much one cupcake would cost.

We can determine the relationship between the values by creating a ratio of number of cupcakes to cost:

Where 
We can now solve for 
The cost of one cupcake is then
Example Question #31 : Data Analysis
Students were asked if they prefer TV or radio. The following Venn Diagram depicts the number of students who said TV, radio, or both. How many students like both TV and radio?
12
22
15
7
7
The blue circle of the Venn diagram depicts the number of students who prefer TV, the orange circle depicts the number of students who prefer radio, and the region of overlap indicates the number of students who like both. Therefore, 7 students like both TV and radio.
Example Question #2 : How To Find The Common Part With A Venn Diagram

Aracely posted a survey question using one of her social network accounts. She grouped the results into three categories. The response results are represented by the Venn diagram shown above.
Group 

What percentage of the respondents answered "maybe" to Aracely's survey question?





The overlapping portion of the Venn diagram represents the percentage of respondents that answered "maybe" to Aracely's survey question.
Since the diagram shows that exactly 

The solution is the total percent population take away the percent that answered "yes" or "no":
All ISEE Lower Level Quantitative Resources