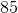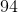ISEE Lower Level Quantitative : How to find the missing part of a list
Study concepts, example questions & explanations for ISEE Lower Level Quantitative
All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #61 : Data Analysis And Probability
What is the next number in the series?
First, determine what the pattern is in the series. The pattern here is to multiply the previous number by 2 and then add 1. Therefore, multiply 47 by 2 (which is 94), and then add 1. The result is 95.
Example Question #62 : Data Analysis And Probability
What is the missing value of w in this sequence?
In this sequence, every subsequent number is 7 less than the preceding number. Given that the number that precedes w is 71, the value of w is 
Example Question #63 : Data Analysis And Probability
What is the value of n in the sequence below?
The numbers increase by 5. Given that the number before n is 20, the value of n is 
Example Question #2 : How To Find The Next Term In An Arithmetic Sequence
What is the next term in the following sequence?
What is the next term in the following sequence?
This is an arithmetic sequence with a common difference of 
Example Question #4 : How To Find The Missing Part Of A List
Find the missing number in the sequence:
In this sequence, the difference between each number is double the difference between the number that came prior to it in the sequence. For example, 
Example Question #1 : How To Find The Missing Part Of A List
What is the missing number in the following list:
In this sequence of numbers, there is an important pattern to recognize. In this sequence each number is a prime number, however the sequence skips every other prime number. Thus, the sequence begins with the prime number 
Example Question #1 : How To Find The Missing Part Of A List
Find the missing number in this set:
In this sequence of numbers, there is an important pattern to recognize. Each number in this sequence is a composite number--however, the sequence skips every other composite number. Thus, the next composite number after 
Example Question #71 : Data Analysis And Probability
Find the next number in the list:
In this sequence of numbers, there is an important pattern to recognize. Each number is greater than the number prior to it by a margin of 
Example Question #72 : Data Analysis And Probability
Find the missing number:
In this sequence of numbers, there is an important pattern to recognize. Each number is greater than the number prior to it by a margin of 
Example Question #73 : Data Analysis And Probability
Find the missing number in the list below:
In this sequence of numbers, there is an important pattern to recognize. Each number is greater than the number prior to it by a margin of 9. Thus, the correct answer is 
Certified Tutor
Certified Tutor
All ISEE Lower Level Quantitative Resources
