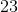We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : How to find a line on a coordinate plane

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find A Line On A Coordinate Plane

Vt_custom_xy_xylinesegment1

Which equation of a line is parallel to line segment $\bar{AB}$ ?

Possible Answers:

$y=\frac{9}{13}-8$

$y=-\frac{9}{13}-6$

$y=\frac{13}{9}+5$

$y=\frac{5}{12}+4$

Correct answer:

$y=\frac{9}{13}-8$

Explanation:

In order for the equation to represent a line that is parallel to the line that is shown, the equation must have the same slope as line segment $\bar{AB}$ .

Since, line segment $\bar{AB}$ has a slope of $\frac{9}{13}$ , the correct equation is: $y=\frac{9}{13}-8$

Report an Error

Example Question #1 : How To Find A Line On A Coordinate Plane

Vt_custom_xy_xysegment_3

The points in the above line segment are apart of which of the following linear equations?

Possible Answers:

x=7

y=7

y=-7

x=-7

Correct answer:

y=-7

Explanation:

The above line segment is a horizontal line that passes through the axis at -7. Since this line is horizontal, it does not have a slope. Therefore, y=-7 is the correct answer.

Report an Error

Example Question #1 : How To Find A Line On A Coordinate Plane

Vt_custom_xy_xysegment_3

Which of the following linear equations is perpendicular to the line segment shown above?

Possible Answers:

x=-3

$y=-\frac{1}{2}-7$

y=-7

y=7

Correct answer:

x=-3

Explanation:

Since the line segment is horizontal, the equation that is perpendicular to the segment must run vertically. The only linear equation that runs vertically (perpendicular to y=-7 ) is x=-3 .

Report an Error

Example Question #2 : How To Find A Line On A Coordinate Plane

Vt_custom_xy_xysegment_3

At what coordinate point does the line x=-3 intersect with the line segment shown above?

Possible Answers:

(-3,-7)

(3,-7)

(-7,-3)

(3,7)

Correct answer:

(-3,-7)

Explanation:

Since, x=-3 is perpendicular to y=-7 the points must cross at (-3,-7) , because it is the only coordinate point that both lines pass through.

Report an Error

Example Question #3 : How To Find A Line On A Coordinate Plane

Vt_custom_xy_xyline5

At which coordinate point does this line segment cross the -axis?

Possible Answers:

(3,0)

(0,3)

(-3,0)

(0,-2)

Correct answer:

(3,0)

Explanation:

Keep in mind that the values in the coordinate points are (x,y) , thus the point (3,0) is the point at which the line segment passes through the axis.

Report an Error

Example Question #6 : How To Find A Line On A Coordinate Plane

Find the equation that represents a line that has a intercept of .

Possible Answers:

$y=\frac{3}{4}x+7$

$y=\frac{3}{4}x+5$

$y=\frac{3}{4}x-7$

$y=\frac{3}{4}x-5$

Correct answer:

$y=\frac{3}{4}x-7$

Explanation:

To identify the correct equation, apply the formula y=mx+b , where represents the slope of the line and the intercept.

Thus, the line that passes through the axis at (0,-7) is $y=\frac{3}{4}x-7$

Report an Error

Example Question #7 : How To Find A Line On A Coordinate Plane

Which of the following equations of a line has the steepest slope?

Possible Answers:

$y=-\frac{3}{4}x+8$

$y=-\frac{3}{8}x+4$

$y=\frac{8}{4}x+4$

$y=-\frac{8}{3}x+4$

Correct answer:

$y=-\frac{8}{3}x+4$

Explanation:

To find which equation of a line has the steepest slope, apply the formula: y=mx+b , where represents the slope of the line and represents the intercept.

Also, note that $m=\frac{rise}{run}$ , meaning the change in the value, over the change in the value.

The equation that has the largest absolute value of m is the equation that has the steepest slope.

Thus, the equation $y=-\frac{8}{3}x+4$ has the steepest slope, because in order to go from one point to the next move a vertical distance of and a horizontal distance of which is larger than any of the other choices.

Report an Error

Example Question #1 : How To Find A Line On A Coordinate Plane

Find the slope of the line that passes through the coordinate points (-3,4) and (2,-1) .

Possible Answers:

$\frac{1}{2}$

$-\frac{1}{2}$

Correct answer:

Explanation:

To find the slope of the line that passes through these two coordinate points, apply the formula:

$Slope=\frac{y_2-y_1}{x_2-x_1}$

Thus the correct answer is:

$\frac{ -1-4}{2--3}=\frac{-5}{5}=-\frac{5}{5}=-1$

Report an Error

Example Question #9 : How To Find A Line On A Coordinate Plane

Vt_custom_xy_xylinesegment1

Line segment $\bar{AB}$ has endpoints (-6,-3) and (7,6) . What is the slope of the line segment?

Possible Answers:

$-\frac{9}{13}$

$\frac{9}{13}$

$\frac{1}{3}$

$\frac{13}{9}$

Correct answer:

$\frac{9}{13}$

Explanation:

To find the slope of the line that passes through these two coordinate points, apply the formula:

$Slope=\frac{y_2-y_1}{x_2-x_1}$

Thus the correct answer is:
$\frac{6--3}{7--6}=\frac{6+3}{7+6}=\frac{9}{13}$

Report an Error

Example Question #10 : How To Find A Line On A Coordinate Plane

Vt_custom_xy_xysegment_3

Find the length of the line segment above.

Possible Answers:

Correct answer:

Explanation:

To find the length of this line segment find the difference between each of the two end points values, since they have the same value.

The difference between and is .

9-(-8)=9+8=17

Report an Error

View Tutors

Pamela
Certified Tutor

University of Colorado Boulder, Bachelor of Science, International Marketing.

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Ericka
Certified Tutor

Southern Nazarene University, Bachelors, Network Engineering and Management . Oklahoma State University-Main Campus, Master o...

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Los Angeles, Computer Science Tutors in Los Angeles, Computer Science Tutors in Denver, Spanish Tutors in Boston, ACT Tutors in Seattle, Algebra Tutors in Philadelphia, Statistics Tutors in Phoenix, LSAT Tutors in Dallas Fort Worth, Chemistry Tutors in San Diego, Chemistry Tutors in Miami

Popular Courses & Classes

LSAT Courses & Classes in Denver, GMAT Courses & Classes in Denver, SAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Seattle, ACT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Boston, LSAT Courses & Classes in Miami, ACT Courses & Classes in New York City, ACT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Chicago

Popular Test Prep

GMAT Test Prep in Dallas Fort Worth, ACT Test Prep in Dallas Fort Worth, SAT Test Prep in Philadelphia, GMAT Test Prep in Boston, SAT Test Prep in Chicago, GRE Test Prep in Chicago, LSAT Test Prep in Washington DC, SSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Boston, MCAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : How to find a line on a coordinate plane

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #1 : How To Find A Line On A Coordinate Plane

Example Question #1 : How To Find A Line On A Coordinate Plane

Example Question #1 : How To Find A Line On A Coordinate Plane

Example Question #2 : How To Find A Line On A Coordinate Plane

Example Question #3 : How To Find A Line On A Coordinate Plane

Example Question #6 : How To Find A Line On A Coordinate Plane

Example Question #7 : How To Find A Line On A Coordinate Plane

Example Question #1 : How To Find A Line On A Coordinate Plane

Example Question #9 : How To Find A Line On A Coordinate Plane

Example Question #10 : How To Find A Line On A Coordinate Plane

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: