All Intermediate Geometry Resources
Example Questions
Example Question #9 : How To Find An Angle In An Acute / Obtuse Isosceles Triangle
In an obtuse isosceles triangle the largest angle is 






Isosceles triangles always have two equivalent interior angles, and all three interior angles of any triangle always have a sum of 
The solution is:
Example Question #1 : How To Find An Angle In An Acute / Obtuse Isosceles Triangle
In an acute isosceles triangle the measurement of the non-equivalent interior angle is 




Isosceles triangles always have two equivalent interior angles, and all three interior angles of any triangle always have a sum of 
The solution is:
Example Question #41 : Acute / Obtuse Isosceles Triangles
In an obtuse isosceles triangle, the largest interior angle is 





Isosceles triangles always have two equivalent interior angles, and all three interior angles of any triangle always have a sum of 
The solution is:
Example Question #11 : How To Find An Angle In An Acute / Obtuse Isosceles Triangle
You are flying a kite at an altitude of 40 feet after having let out 75 feet of string. What is the kite's angle of elevation from where you are holding the spool of string at a height of 4 feet off the ground? Round answer to one decimal place.
First, we must draw a picture to include all important parts given in the problem.

Once this is determined we can use trigonometry to find the angle of elevation.
Use the inverse sin on a calculator to solve.
Example Question #481 : Intermediate Geometry
Two angles in an isosceles triangle are 50 and 80 degrees respectively. What is the measure of the third angle?
If a triangle is isosceles, two of the angles must be congruent. So the angle must be either 50 degrees or 80 degrees.
We know that the three angles in all triangles must sum to equal 180 degrees. The only answer choice that is both the same as one of the given angles and results in a sum equal to 180 degrees is the 50 degree angle.
50+50+80=180.
Example Question #44 : Acute / Obtuse Isosceles Triangles
An isosceles triangle has one angle measuring 






An isosceles triangle has 2 congruent angles and then a third angle. These angles, as in any triangle, must add to 180.
One possibility is that the 25-degree angle is the "different" one, and the other two are congruent. This could be expressed using the algebraic expression 


The other possibility is that there are 2 25-degree angles and then some different angle measure. This could be expressed using the algebraic expression 

Example Question #482 : Intermediate Geometry

Refer to the above triangle. By what statement does it follow that 
The Converse of the Isosceles Triangle Theorem
The Side-Angle-Side Postulate
The Side-Side-Side Postulate
The Pythagorean Theorem
The Isosceles Triangle Theorem
The Isosceles Triangle Theorem
We are given that, in 


Example Question #41 : Acute / Obtuse Isosceles Triangles

Refer to the above diagram. 


The Side-Angle-Side Postulate
The Side-Side-Side Postulate
The Converse of the Isosceles Triangle Theorem
The Isosceles Triangle Theorem
The Hinge Theorem
The Side-Side-Side Postulate
In addition to the fact that 



Example Question #41 : Acute / Obtuse Isosceles Triangles
Given: 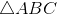

Which statement(s) must be true?
(a)
(b)
(a) but not (b)
(b) but not (a)
(a) and (b)
Neither (a) nor (b)
Neither (a) nor (b)
Neither similarity nor congruence of the two triangles follows from the statements given, as can be seen from the figure below:
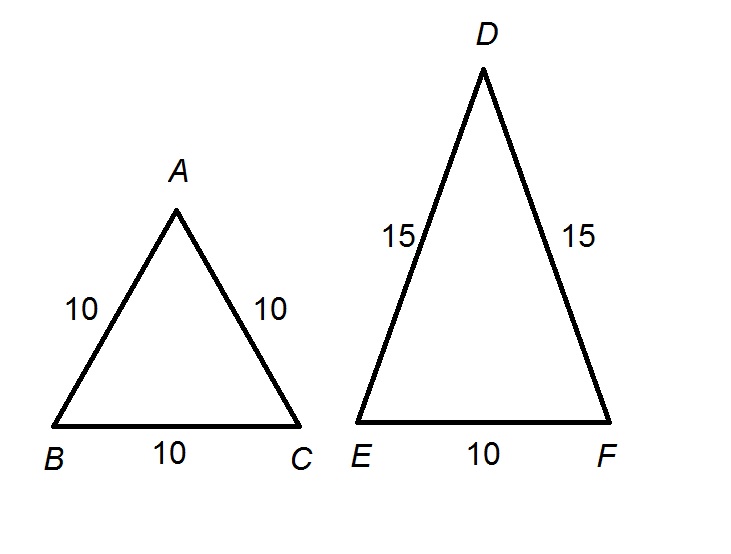

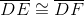

and

The triangles are not similar, and thus cannot be congruent either, so neither statement holds.
Example Question #491 : Plane Geometry
Find the perimeter of the triangle below.

Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.
Certified Tutor
Certified Tutor
All Intermediate Geometry Resources