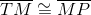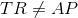All Intermediate Geometry Resources
Example Questions
Example Question #11 : How To Find The Length Of The Side Of A Trapezoid

Using the isosceles trapezoid shown above, find a possible base measurement for a similar trapezoid where the largest base measurement is 
Not enough information is provided.
In order for two trapezoids to be similar their corresponding sides must have the same ratio. Since the largest base length in the image is 


The smaller base shown in the image has a length of 

Example Question #272 : Intermediate Geometry

Using the image shown above, find the lenght for one of the two nonparallel equivalent sides for a similar trapezoid where the perimeter is equal to 
In order for two trapezoids to be similar their corresponding sides must have the same ratio. Since the perimeter in the image is 


The nonparallel equivalent sides shown in the image have a length of 

Example Question #273 : Intermediate Geometry

Using the trapezoid shown above, find the length of side 
In order to find the length of side 





Thus, the solution can be found by applying the formula: 
Example Question #274 : Intermediate Geometry
An isosceles trapezoid has base measurements of 




To solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. Since this problem provides the length for both of the bases as well as the total perimeter, the missing sides can be found using the following formula: Perimeter= Base one 


Note: once you find the answer in inches, convert that quantity to an equivalent amount in feet.
Thus, the solution is:



Example Question #275 : Intermediate Geometry
Quadrilateral 



Rectangle
Isosceles trapezoid
Non-isosceles trapezoid
Kite
Rhombus
Isosceles trapezoid
Quadrilateral 










Example Question #276 : Intermediate Geometry
Given Trapezoid 






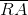
True, false, or undetermined: Trapezoid 

False
Undetermined
True
False
The fact that the trapezoid is isosceles is actually irrelevant. Since 



and
It follows that
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
Assume that 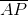


Since the bases are of unequal length, 
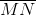
Since 
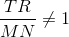
and

This disproves similarity, since one condition is that corresponding sides must be in proportion.
Example Question #1 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the degree measure of 

In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 


Example Question #2 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the angle measurement of 

In a trapezoid, all the interior angles add up to 


Example Question #3 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the angle measurement of 

All the interior angles in a trapezoid add up to 


Example Question #4 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the angle measurement of 

All the interior angles in a trapezoid add up to 


All Intermediate Geometry Resources