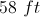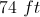Intermediate Geometry : Plane Geometry
Study concepts, example questions & explanations for Intermediate Geometry
All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the degree measurement of 
Cannot be determined from the given information.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
Example Question #1 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the degree measurement of 
Cannot be determined from the information given.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
Example Question #4 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the degree measurement of 
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
Example Question #1 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the degree measurement of 
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
Example Question #2 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the degree measurement of 
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
Therefore, we can write the following equation and solve for a.
Example Question #3 : How To Find An Angle In A Trapezoid
In the trapezoid below, find the degree measurement of 
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
Therefore, we can write the following equation and solve for z.
Example Question #281 : Intermediate Geometry
In the trapezoid below, find the degree measurement of 
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
Therefore, we can write the following equations and solve for y.
Example Question #282 : Plane Geometry
In the trapezoid below, find the degree measurement of 
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
Thus, we can write the following equation and solve for x.
Example Question #1 : How To Find The Perimeter Of A Trapezoid
Find the perimeter of the following trapezoid.
The answer is 50 ft. In order to find the perimeter, you must find the length of the left side. After some deduction 
Once you find that the last side is 8 ft, you can add
to get an answer of 50 ft. for the perimeter.
Example Question #2 : How To Find The Perimeter Of A Trapezoid
The height of a trapezoid is 
Find the perimeter of the trapezoid to the nearest hundreth.
Use the triangle formed by the height of the trapezoid to find the lengths of the two sides of the trapezoid and the length of 
This finds the base of the triangle, which can be added twice to 
Now, use the same triangle to find the length of the sides.
Lastly, add all of the lengths together: 
Certified Tutor
Certified Tutor
All Intermediate Geometry Resources
