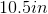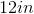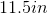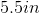Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Quadrilaterals

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #311 : Plane Geometry

Vt_custom_kite_series_int._geo

Using the kite shown above, find the length of side

Possible Answers:

18cm

11cm

21cm

9cm

$\frac{21}{2}cm$

Correct answer:

18cm

Explanation:

To find the missing side of this kite, work backwards using the formula:

p=2(a+b) , where and represent the length of one side from each of the two pairs of adjacent sides.

The solution is:

58=2(11+b)

$\frac{58}{2}=11+b$

29=11+b

b=29-11=18

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Kite

Vt_custom_kite_series_cont._

Using the kite shown above, find the length of side . (Note, the perimeter of this kite is equal to 2.5 feet).

Possible Answers:

$\frac{3}{4}ft$

1.5ft

4ft

1.25ft

$\frac{12}{5}in$

Correct answer:

$\frac{3}{4}ft$

Explanation:

To find the missing side of this kite, work backwards using the formula:

p=2(a+b) , where and represent the length of one side from each of the two pairs of adjacent sides.

The solution is:

2.5 feet=2(0.5 foot+b)

$\frac{2.5}{2}=(0.5+b)$

1.25=0.5+b

$b=1.25-0.5=0.75=\frac{3}{4}$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Kite

Ms. Dunn has a kite shaped backyard with a perimeter of yards. One pair of adjacent sides of the kite-shaped backyard each have lengths of yard. What is the measurement for one of the other two sides of the kite-shaped backyard?

Possible Answers:

7yds

24yds

23yds

26yds

18yds

Correct answer:

23yds

Explanation:

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Kite

A kite has a perimeter of 138 mm. One pair of adjacent sides of the kite have lengths of mm. What is the measurement for one of the other two sides of the kite?

Possible Answers:

105mm

69mm

26mm

36mm

79mm

Correct answer:

36mm

Explanation:

To find the missing side of this kite, work backwards using the formula:

p=2(a+b) , where and represent the length of one side from each of the two pairs of adjacent sides.

The solution is:

138=2(33+b)

$\frac{138}{2}=33+b$

69=33+b

b=69-33=36

Report an Error

Example Question #4 : How To Find The Length Of The Side Of A Kite

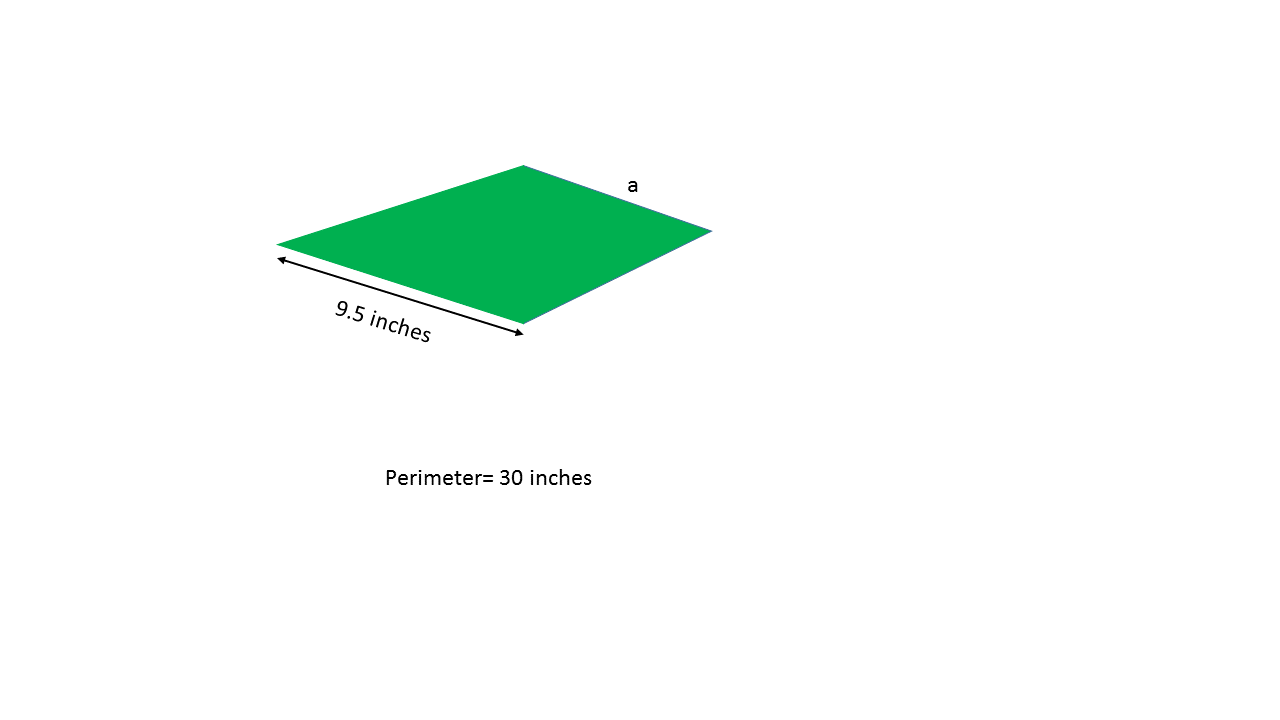
Kite_series_cont....

Using the above kite, find the length of side .

Possible Answers:

10.5in

12in

5in

11.5in

5.5in

Correct answer:

5.5in

Explanation:

To find the missing side of this kite, work backwards using the formula:

p=2(a+b) , where and represent the length of one side from each of the two pairs of adjacent sides.

The solution is:

30=2(9.5+a)

30=19+2a

2a=30-19=11

$a=\frac{11}{2}=5.5$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Kite

The lengths of the non-adjacent sides of a kite have the ratio 4:1 . If the longer sides have a length of cm, what is the length of each of the shorter two sides?

Possible Answers:

3cm

$\frac{4}{12}cm$

19cm

1.5cm

4cm

Correct answer:

3cm

Explanation:

The sides have the ratio 4:1 , thus the longer sides must be times greater than the smaller sides.

Since the longer sides are cm, the shorter sides must be:

$12\div4=3$

Report an Error

Example Question #151 : Quadrilaterals

A kite has a perimeter of 214 mm. One pair of adjacent sides of the kite have lengths of mm. What is the measurement for one of the other two sides of the kite?

Possible Answers:

107mm

41mm

55mm

53mm

71mm

Correct answer:

55mm

Explanation:

To find the missing side of this kite, work backwards using the formula:

p=2(a+b) , where and represent the length of one side from each of the two pairs of adjacent sides.

The solution is:

214=2(52+b)

$\frac{214}{2}=(52+b)$

107=52+b

b=107-52=55

Report an Error

Example Question #152 : Quadrilaterals

Kite_pic_custom_vt

Find the longest side of the kite that is shown above.

Possible Answers:

89in

93in

$\frac{91}{2}in$

83in

81in

Correct answer:

83in

Explanation:

To find the missing side of this kite, work backwards using the formula:

p=2(a+b) , where and represent the length of one side from each of the two pairs of adjacent sides.

The solution is:

324=2(79+b)

$\frac{324}{2}=(79+b)$

162=(79+b)

b=162-79=83

Report an Error

Example Question #153 : Quadrilaterals

A kite has a perimeter of $3\frac{1}{2}$ feet. One pair of adjacent sides of the kite have lengths of foot each. What is the measurement for one of the other two sides of the kite?

Possible Answers:

$\frac{1}{4}ft$

$\frac{3}{4}ft$

$1\frac{1}{4}ft$

$\frac{2}{3}ft$

$1\frac{1}{3}ft$

Correct answer:

$\frac{3}{4}ft$

Explanation:

To solve this problem use the formula p=2(a+b) , where and represent the length of one side from each of the two pairs of adjacent sides.

The solution is:

$3\frac{1}{2}=2(1+b)$

$3\frac{1}{2}\div2=1+b$

Make the first fraction into an improper fraction. Then find the reciprocal of the denominator and switch the operation sign:

$3\frac{1}{2}\times\frac{1}{2}$

$\frac{7}{2}\times \frac{1}{2}=1+b$

$\frac{7}{4}=1+b$

$b=\frac{7}{4}-\frac{4}{4}=\frac{3}{4}$

Report an Error

Example Question #11 : How To Find The Length Of The Side Of A Kite

Given: Regular Pentagon PENTA with center . Construct segments $\overline{CP}$ and $\overline{CN}$ to form Quadrilateral CPEN .

True or false: Quadrilateral CPEN is a kite.

Possible Answers:

False

True

Correct answer:

True

Explanation:

Below is regular Pentagon PENTA with center , a segment drawn from to each vertex - that is, each of its radii drawn.

Pentagon a

A kite is a quadrilateral with two sets of congruent adjacent sides, with the common length of one pair differing from that of the other. A regular polygon has congruent sides, so $\overline{EN} \cong \overline{EP}$ ; also, all radii of a regular polygon are congruent, so $\overline{CP} \cong \overline{CN}$ . It follows by definition that Quadrilateral CPEN is a kite.

Report an Error

View Tutors

Dante
Certified Tutor

New Jersey Institute of Technology, Bachelor of Science, Electrical Engineering. Stevens Institute of Technology, Master of S...

View Tutors

Kaela
Certified Tutor

Xavier University, Bachelor of Science, Environmental Science. Miami University-Middletown, Master of Science, Biology, Gener...

View Tutors

Michael
Certified Tutor

Furman University, Bachelor in Arts, History. Covenant Theological Seminary, Master of Divinity, Theology.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Seattle, Spanish Tutors in San Diego, Biology Tutors in Philadelphia, SSAT Tutors in Chicago, French Tutors in Los Angeles, ACT Tutors in Washington DC, French Tutors in Miami, MCAT Tutors in Boston, Math Tutors in Houston, Reading Tutors in Houston

Popular Courses & Classes

LSAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Chicago, GRE Courses & Classes in Seattle, ACT Courses & Classes in Houston, SAT Courses & Classes in Atlanta, GMAT Courses & Classes in Boston, SAT Courses & Classes in Philadelphia, GRE Courses & Classes in Boston, SSAT Courses & Classes in San Diego, GRE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SAT Test Prep in New York City, ACT Test Prep in Philadelphia, GMAT Test Prep in Boston, GRE Test Prep in Los Angeles, ISEE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Houston, SAT Test Prep in Denver, LSAT Test Prep in Chicago, MCAT Test Prep in Chicago, SAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Quadrilaterals

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #311 : Plane Geometry

Example Question #2 : How To Find The Length Of The Side Of A Kite

Example Question #1 : How To Find The Length Of The Side Of A Kite

Example Question #1 : How To Find The Length Of The Side Of A Kite

Example Question #4 : How To Find The Length Of The Side Of A Kite

Example Question #1 : How To Find The Length Of The Side Of A Kite

Example Question #151 : Quadrilaterals

Example Question #152 : Quadrilaterals

To find the missing side of this kite, work backwards using the formula:

Example Question #153 : Quadrilaterals

Example Question #11 : How To Find The Length Of The Side Of A Kite

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: