Intermediate Geometry : Parallel Lines
Study concepts, example questions & explanations for Intermediate Geometry
All Intermediate Geometry Resources
Example Questions
Example Question #11 : Parallel Lines
Where do the lines 
They never intersect.
They never intersect.
By solving both equations to standard form 
Example Question #12 : How To Find Out If Lines Are Parallel
A line passes through both the coordinates 
The line has a slope of 
Example Question #12 : How To Find Out If Lines Are Parallel
Choose the equation that represents a line that is parallel to 
Two lines are parallel if and only if they have the same slope. To find the slopes, we must put the equations into slope-intercept form, 
Example Question #184 : Coordinate Geometry
Which of the following lines are parallel?
None of these.
None of these.
None of these lines are parallel.
In order for lines to be parallel, the lines must NEVER cross. Lines with identical slopes never cross. An example of two parallel lines would be:
Note that only the slope determines if line are parallel.
Example Question #187 : Lines
Are the lines of the equations
and
parallel, perpendicular, or neither?
Neither
Perpendicular
Parallel
Parallel
Write each equation in the slope-intercept form 
The first equation,
is in the slope-intercept form 
The slope of the line of this equation is the 
The lines of both equations have the same slope, 
Example Question #12 : How To Find Out If Lines Are Parallel
The slopes of two lines on the coordinate plane are 0.333 and 
True or false: the lines are parallel.
True
False
False
Two lines are parallel if and only if they have the same slope. The slope of one of the lines is 0.333. The other line has slope 
Example Question #191 : Lines
One line on the coordinate plane has its intercepts at 
Perpendicular
Parallel
Neither
Perpendicular
To answer this question, we must determine the slopes of both lines. If a line has as its intercepts 
The first line has as its slope
The second line has as its slope
Two lines are parallel if and only if their slopes are equal; this is not the case.
They are perpendicular if and only if the product of their slopes is 
so they are perpendicular.
Example Question #13 : How To Find Out If Lines Are Parallel
The slopes of two lines on the coordinate plane are 0.75 and 
True or false: The lines are parallel.
True
False
True
Two lines are parallel if and only if they have the same slope. The slope of one of the lines is 
Example Question #192 : Lines
A line which includes the point 
Which of these points is on that line?
Write the given equation in slope-intercept form:
The given line has slope 
We can use the slope formula 
The only point whose inclusion yields a line with slope 
Example Question #1 : How To Find The Slope Of Parallel Lines
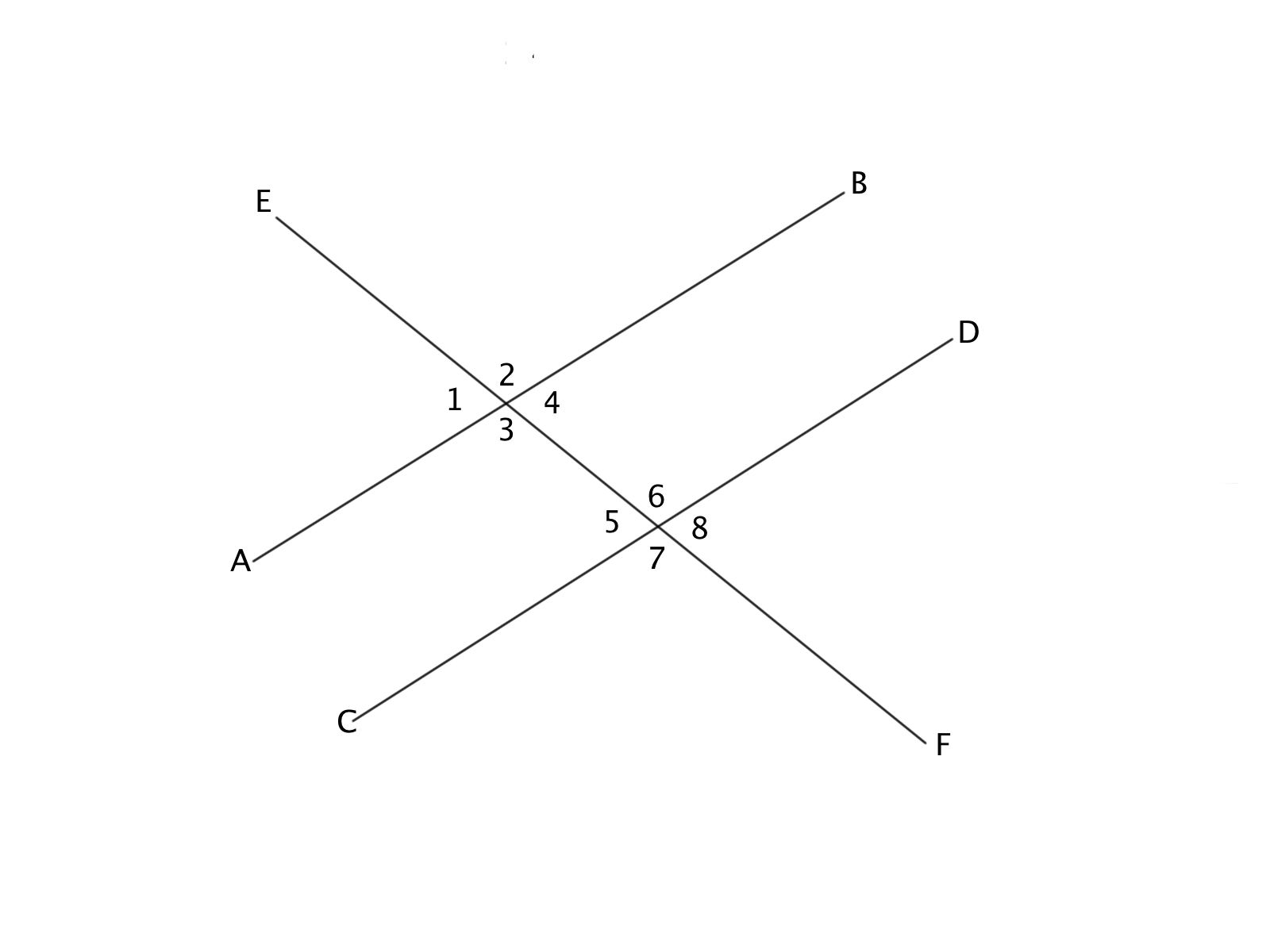
If the slope of line AB is 3x, and Angle 1 and Angle 8 are congruent, what is the slope of line CD, and why?
(1/3)x, because of the Vertical Angle Theorem
3x, because of the Vertical Angle Theorem
3x, because of the Corresponding Angle Theorem
3x, because of the Alternate Exterior Angle Theorem
(1/3)x, because of the Alternate Exterior Angle Theorem
3x, because of the Vertical Angle Theorem
Angles 1 and 8 are a vertical pair. If these angles are congruent, it means that lines AB and CD are parallel based on the Vertical Angle Theorem. Parallel lines have the same slope, so the slope of CD is 3x.
All Intermediate Geometry Resources
