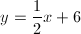Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Parallel Lines

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 Next →

Example Question #21 : Parallel Lines

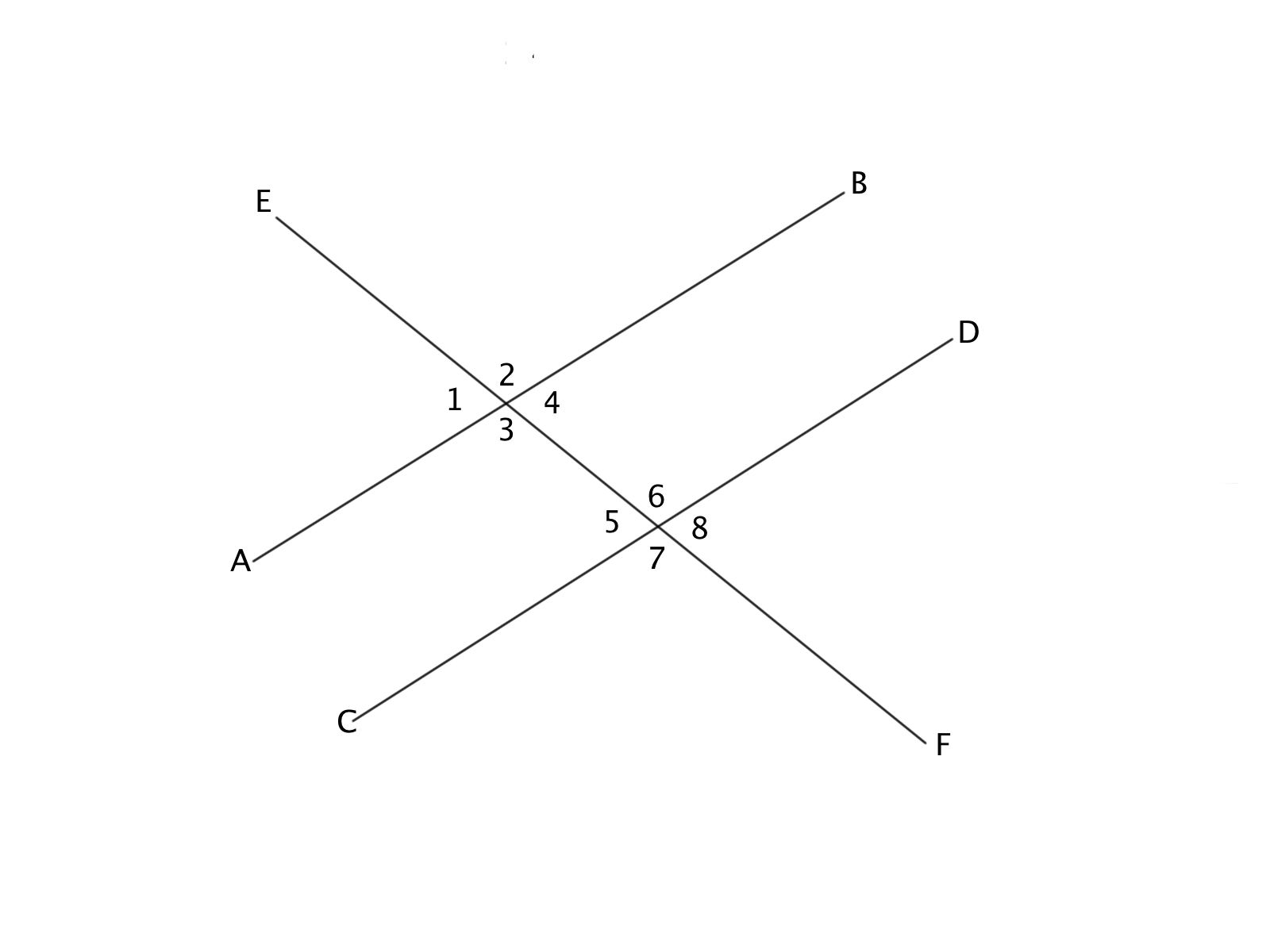
Transverselinestilted

The slope of line CD is 4x, and Angle 1 and Angle 5 are congruent. What is the slope of line AB and why?

Possible Answers:

4x, because of Corresponding Angles Theorem

(1/4)x, because of the Corresponding Angle Theorem

4x, because of Alternate Interior Angles Theorem

4x, because of the Vertical Angle Theorem

There is not enough information to determine

Correct answer:

4x, because of Corresponding Angles Theorem

Explanation:

Parallel lines have the same slope. If Angles 1 and 5 are congruent, then lines AB and CD have the same slope (4x) based on the Congruent Angles Theorem.

Report an Error

Example Question #1 : How To Find The Slope Of Parallel Lines

Any line that is parallel to 6x-2y=4 must have a slope of what?

Possible Answers:

-1/3

1/3

Correct answer:

Explanation:

Two lines are parallel if and only if they have the same slope. To find the slope, we must put the equation into slope-intercept form, y=mx+b , where equals the slope of the line. First, we must subtract from each side of the equation, giving us -2y=-6x+4 . Next, we divide both sides by , giving us y=3x-2 . We can now see that the slope is .

Report an Error

Example Question #191 : Coordinate Geometry

Suppose the equation of the first line is -3x+y=4 . What must be the value of to make the second equation -kx=4+y parallel to the first line?

Possible Answers:

$\frac{3}{4}$

$\frac{4}{3}$

$-\frac{3}{4}$

Correct answer:

Explanation:

Rewrite both equations so that they are in slope-intercept form, y=mx+b .

For the first equation:

-3x+y=4

y=3x+4

The slope of the first line is .

m=3

Rewrite the second equation in slope-intercept form:

-kx=4+y

-kx -4=y

The value of must be equal to three to be parallel. Solve for .

-k=3

k=-3

Report an Error

Example Question #2 : How To Find The Slope Of Parallel Lines

If the equation of one line is $\frac{1}{10}x-10y = 1$ , what must be the slope of another line so that both lines are parallel to each other?

Possible Answers:

$\frac{1}{10}$

$\frac{1}{100}$

$-\frac{1}{100}$

Correct answer:

$\frac{1}{100}$

Explanation:

Rewrite the equation of the first line in slope-intercept form, y=mx+b .

$\frac{1}{10}x-10y = 1$

$\frac{1}{10}x = 1+10y$

$\frac{1}{10}x-1 = 10y$

$y=\frac{1}{100}x -\frac{1}{10}$

The value of the slope, , can be seen as $\frac{1}{100}$ . For another line to be parallel to this line, their slopes must be the same.

Report an Error

Example Question #6 : How To Find The Slope Of Parallel Lines

Find a line parallel to the line with the equation:

y=10x-2

Possible Answers:

y=10x+14

$y=\frac{1}{10}x-2$

$y=-\frac{1}{10}x+2$

y=-10x-2

Correct answer:

y=10x+14

Explanation:

For two lines to be parallel, they must have the same slope. For a line in y=mx+b , or slope intercept form, corresponds to the slope of the line.

For the given line, m=10 . A line that is parallel must also then have the same slope.

Only the following line has the same slope:

y=10x+14

Report an Error

Example Question #7 : How To Find The Slope Of Parallel Lines

Find a line parallel to the line with the equation:

y=19x-14

Possible Answers:

y=14x+19

y=19x+2

$y=\frac{1}{19}x+14$

y=-19x-2

Correct answer:

y=19x+2

Explanation:

For two lines to be parallel, they must have the same slope. For a line in y=mx+b , or slope intercept form, corresponds to the slope of the line.

For the given line, m=19 . A line that is parallel must also then have the same slope.

Only the following line has the same slope:

y=19x+2

Report an Error

Example Question #8 : How To Find The Slope Of Parallel Lines

Find a line parallel to the line with the equation:

y=129x-200

Possible Answers:

y=-129x+200

y=200x-129

$y=\frac{1}{129}x-2001$

y=129x+41

Correct answer:

y=129x+41

Explanation:

For two lines to be parallel, they must have the same slope. For a line in y=mx+b , or slope intercept form, corresponds to the slope of the line.

For the given line, m=129 . A line that is parallel must also then have the same slope.

Only the following line has the same slope:

y=129x+41

Report an Error

Example Question #9 : How To Find The Slope Of Parallel Lines

Find a line parallel to the line with the equation:

$y=\frac{1}{365}x-2$

Possible Answers:

y=365x-10

$y=\frac{x}{365}+4$

$y=-\frac{x}{365}+120$

y=-25x+124

Correct answer:

$y=\frac{x}{365}+4$

Explanation:

For two lines to be parallel, they must have the same slope. For a line in y=mx+b , or slope intercept form, corresponds to the slope of the line.

For the given line, $m=\frac{1}{365}$ . A line that is parallel must also then have the same slope.

Only the following line has the same slope:

$y=\frac{x}{365}+4$

Report an Error

Example Question #1 : How To Find The Equation Of A Parallel Line

What is the equation of a line that is parallel to the line $\small y=\frac{1}{2}x+3$ and includes the point (4, 2) ?

Possible Answers:

$\small y=\frac{1}{2}x+6$

$\small y=\frac{1}{2}x$

$\small y=2x-6$

$\small y=-2x+10$

Correct answer:

$\small y=\frac{1}{2}x$

Explanation:

The line parallel to $\small y=\frac{1}{2}x+3$ must have a slope of $\frac{1}{2}$ , giving us the equation $\small y=\frac{1}{2}x+b$ . To solve for b, we can substitute the values for y and x.

$\small 2=(\frac{1}{2})(4)+b$

$\small 2=2+b$

$\small b=0$

Therefore, the equation of the line is $\small y=\frac{1}{2}x$ .

Report an Error

Example Question #1 : How To Find The Equation Of A Parallel Line

Suppose a line y=2x . What is the equation of a parallel line that intersects point (1,3) ?

Possible Answers:

y=2x+1

y=2x+4

y=2x+2

y=2x+3

y=2x+5

Correct answer:

y=2x+1

Explanation:

A line parallel to y=2x must have a slope of two. Given the point (1,3) and the slope, use the slope-intercept formula to determine the -intercept by plugging in the values of the point and solving for :

y=mx+b

3=(2)(1)+b

3=2+b

3-2=2+b-2

b=1

Plug the slope and the -intercept into the slope-intercept formula:

y=2x+1

Report an Error

← Previous 1 2 3 4 Next →

View Tutors

Siavash
Certified Tutor

Ryerson University, Bachelor of Engineering, Civil Engineering. University of Toronto, Master of Engineering, Biomedical Engi...

View Tutors

Lois
Certified Tutor

Saint Johns University, Bachelor of Science, Economics. Saint Johns University, Master of Science, Research and Development M...

View Tutors

John
Certified Tutor

Arizona State University, Bachelor of Science, Microbiology.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Atlanta, English Tutors in Miami, Statistics Tutors in Denver, Reading Tutors in Boston, ISEE Tutors in Phoenix, LSAT Tutors in Philadelphia, GMAT Tutors in Los Angeles, GMAT Tutors in Miami, English Tutors in Denver, ACT Tutors in San Francisco-Bay Area

Popular Courses & Classes

GRE Courses & Classes in Phoenix, GMAT Courses & Classes in New York City, GMAT Courses & Classes in Seattle, Spanish Courses & Classes in Houston, ACT Courses & Classes in Washington DC, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in Houston, LSAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Washington DC, LSAT Courses & Classes in San Diego

Popular Test Prep

LSAT Test Prep in Houston, SSAT Test Prep in Los Angeles, GMAT Test Prep in New York City, SSAT Test Prep in Atlanta, GRE Test Prep in Denver, LSAT Test Prep in Los Angeles, ISEE Test Prep in Los Angeles, ACT Test Prep in Washington DC, SAT Test Prep in Philadelphia, ACT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Parallel Lines

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #21 : Parallel Lines

Example Question #1 : How To Find The Slope Of Parallel Lines

Example Question #191 : Coordinate Geometry

Example Question #2 : How To Find The Slope Of Parallel Lines

Example Question #6 : How To Find The Slope Of Parallel Lines

Example Question #7 : How To Find The Slope Of Parallel Lines

Example Question #8 : How To Find The Slope Of Parallel Lines

Example Question #9 : How To Find The Slope Of Parallel Lines

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #1 : How To Find The Equation Of A Parallel Line

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: