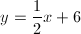We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : How to find the equation of a parallel line

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Equation Of A Parallel Line

What is the equation of a line that is parallel to the line $\small y=\frac{1}{2}x+3$ and includes the point (4, 2) ?

Possible Answers:

$\small y=-2x+10$

$\small y=\frac{1}{2}x$

$\small y=\frac{1}{2}x+6$

$\small y=2x-6$

Correct answer:

$\small y=\frac{1}{2}x$

Explanation:

The line parallel to $\small y=\frac{1}{2}x+3$ must have a slope of $\frac{1}{2}$ , giving us the equation $\small y=\frac{1}{2}x+b$ . To solve for b, we can substitute the values for y and x.

$\small 2=(\frac{1}{2})(4)+b$

$\small 2=2+b$

$\small b=0$

Therefore, the equation of the line is $\small y=\frac{1}{2}x$ .

Report an Error

Example Question #1 : How To Find The Equation Of A Parallel Line

Suppose a line y=2x . What is the equation of a parallel line that intersects point (1,3) ?

Possible Answers:

y=2x+1

y=2x+3

y=2x+4

y=2x+5

y=2x+2

Correct answer:

y=2x+1

Explanation:

A line parallel to y=2x must have a slope of two. Given the point (1,3) and the slope, use the slope-intercept formula to determine the -intercept by plugging in the values of the point and solving for :

y=mx+b

3=(2)(1)+b

3=2+b

3-2=2+b-2

b=1

Plug the slope and the -intercept into the slope-intercept formula:

y=2x+1

Report an Error

Example Question #2 : How To Find The Equation Of A Parallel Line

Find the equation of the line parallel to 3x+3y=1 that passes through the point (2,2) .

Possible Answers:

y=-x-4

y=3x+4

y=3x-4

y=-x+4

y=x-2

Correct answer:

y=-x+4

Explanation:

Write 3x+3y=1 in slope intercept form, y=mx+b , to determine the slope, :

3y=-3x+1

$y=-x+\frac{1}{3}$

The slope is:

m=-1

Given the slope, use the point (2,2) and the equation y=mx+b to solve for the value of the -intercept, . Substitute the known values.

2=(-1)(2)+b

b=4

With the known slope and the -intercept, plug both values back to the slope intercept formula. The answer is y=-x+4 .

Report an Error

Example Question #3 : How To Find The Equation Of A Parallel Line

Given y=3x+20 , find the equation of a line parallel.

Possible Answers:

$y=\frac{1}{3}x-20$

y=-3x-12

y=3x-12

y=0.3x+20

$y=\frac{-1}{3}-20$

Correct answer:

y=3x-12

Explanation:

The definition of a parallel line is that the lines have the same slopes, but different intercepts. The only answer with the same slope is y=3x-12 .

Report an Error

Example Question #4 : How To Find The Equation Of A Parallel Line

Which one of these equations is parallel to:

y=3x+4

Possible Answers:

$y=\frac{-1}{3}+4$

y=3x+1

y=-3x+7

$y=\frac{1}{3}x$

y=4

Correct answer:

y=3x+1

Explanation:

Equations that are parallel have the same slope.

For the equation:

y=3x+4

The slope is since that is how much changes with increment of .

The only other equation with a slope of is:

y=3x+1

Report an Error

Example Question #5 : How To Find The Equation Of A Parallel Line

What equation is parallel to:

y=x

Possible Answers:

y=-x+1

y=2x

y=x+42746

y=0

y=x^2+4

Correct answer:

y=x+42746

Explanation:

To find a parallel line to

y=x

we need to find another equation with the same slope of or .

The only equation that satisfies this is y=x+42746 .

Report an Error

Example Question #6 : How To Find The Equation Of A Parallel Line

What equation is parallel to:

y=5x+5

Possible Answers:

y=5x+10

$y=\frac{1}{5}x+4$

y=x+5

y=4x+3

$y=\frac{-1}{5}x+5$

Correct answer:

y=5x+10

Explanation:

To find an equation that is parallel to

y=5x+5

we need to find an equation with the same slope of .

Basically we are looking for another equation with .

The only other equation that satisfies this is

y=5x+10 .

Report an Error

Example Question #7 : How To Find The Equation Of A Parallel Line

A line is parallel to the line of the equation

5x+ 7y = 32

and passes through the point (-2, 8) .

Give the equation of the line in standard form.

Possible Answers:

7x- 5y= -54

5x+ 7y = 46

5x- 7y = -66

None of the other choices gives the correct response.

7x + 5y= 26

Correct answer:

5x+ 7y = 46

Explanation:

Two parallel lines have the same slope. Therefore, it is necessary to find the slope of the line of the equation

5x+ 7y = 32

Rewrite the equation in slope-intercept form y = mx+ b . , the coefficient of , will be the slope of the line.

Add -5x to both sides:

5x+ 7y + (-5x ) = 32 + (-5x )

7y = -5x+32

Multiply both sides by $\frac{1}{7}$ , distributing on the right:

$\frac{1}{7} \cdot 7y = \frac{1}{7} \cdot( -5x+32)$

$y = -\frac{5}{7}x+\frac{32}{7}$

The slope of this line is $-\frac{5}{7}$ . The slope of the first line will be the same. The slope-intercept form of the equation of this line will be

$y =-\frac{5}{7}x+b$ .

To find , set x = -2 and y = 8 and solve:

$8 =-\frac{5}{7} (-2)+b$

$8 = \frac{10}{7} +b$

$\frac{56}{7} = \frac{10}{7} +b$

Subtract $\frac{10}{7}$ from both sides:

$\frac{56}{7} - \frac{10}{7} = \frac{10}{7} +b - \frac{10}{7}$

$b = \frac{46}{7}$

The slope-intercept form of the equation is $y =-\frac{5}{7}x+ \frac{46}{7}$

To rewrite in standard form with integer coefficients:

Multiply both sides by 7:

$7 y =7\left (-\frac{5}{7}x+ \frac{46}{7} \right )$

$7 y =7\left (-\frac{5}{7}x \right ) +7\left ( \frac{46}{7} \right )$

7 y =-5x +46

Add to both sides:

7 y + 5x =-5x +46 + 5x

5x+ 7y = 46 ,

the correct equation in standard form.

Report an Error

View Tutors

Shifrah
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Biology, General. Massachusetts College of Pharmacy and Health ...

View Tutors

Shakeel
Certified Tutor

View Tutors

Matthew
Certified Tutor

The New School, Master of Philosophy, Philosophy.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Atlanta, ACT Tutors in Denver, GRE Tutors in San Francisco-Bay Area, Reading Tutors in Los Angeles, English Tutors in Phoenix, Physics Tutors in Los Angeles, SAT Tutors in Dallas Fort Worth, Calculus Tutors in Philadelphia, Spanish Tutors in Phoenix, Chemistry Tutors in Atlanta

Popular Courses & Classes

GRE Courses & Classes in Phoenix, SAT Courses & Classes in Denver, ACT Courses & Classes in Washington DC, SSAT Courses & Classes in New York City, MCAT Courses & Classes in Chicago, LSAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Miami, LSAT Courses & Classes in Atlanta, SAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Phoenix

Popular Test Prep

GRE Test Prep in Phoenix, SSAT Test Prep in Phoenix, LSAT Test Prep in Seattle, SAT Test Prep in Miami, ACT Test Prep in Seattle, GRE Test Prep in Chicago, GRE Test Prep in Seattle, MCAT Test Prep in Boston, SSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : How to find the equation of a parallel line

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #2 : How To Find The Equation Of A Parallel Line

Example Question #3 : How To Find The Equation Of A Parallel Line

Example Question #4 : How To Find The Equation Of A Parallel Line

Example Question #5 : How To Find The Equation Of A Parallel Line

Example Question #6 : How To Find The Equation Of A Parallel Line

Example Question #7 : How To Find The Equation Of A Parallel Line

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: