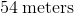We define the variables as \(\displaystyle w = \mbox{width}\) and \(\displaystyle l = \mbox{length} = w + 2\).

We substitute these values into the equation for the area of a rectangle and get \(\displaystyle A_{\mbox{rectangle} }= wl = w(w + 2) = 80\). 

\(\displaystyle w^2 +2w-80=0\)

\(\displaystyle (w - 8)(w + 10) = 0\)

\(\displaystyle w = 8\) or \(\displaystyle w = -10\)

Lengths cannot be negative, so the only correct answer is \(\displaystyle w = 8\). If \(\displaystyle w = 8\), then \(\displaystyle l = 10\). 

Therefore, \(\displaystyle \mbox{perimeter }= 2w + 2l = 16 + 20 = 36\:\mbox{m}\).

To find the perimeter of the square, find the length of the side.  Write the formula to find the length of the side.

\(\displaystyle d=\sqrt{s^2+s^2}\)

Substitute the diagonal and solve for the side.

\(\displaystyle \sqrt2=\sqrt{s^2+s^2}\) 

First, square each side to get rid of the square root. 

\(\displaystyle 2=2s^2\)

Divide 2 by each side to isolate the \(\displaystyle s^2\)

\(\displaystyle 1=s^2\)

Take the square root of each side.

\(\displaystyle 1=s\)

Since there are four sides in a square, multiply the side length by four to get the perimeter.

\(\displaystyle P=4(1)=4\)

The perimeter of an equilateral triangle is three times the length of its side.

\(\displaystyle P=3(-x-4) = -3x-12\)

Write the perimeter formula for a square.

\(\displaystyle P=4s\)

Substitute the side length in the formula and simplify.

\(\displaystyle P=4(a-1)= 4a-4\)

The circumference of a circle is its radius mulitplied by \(\displaystyle 2 \pi\). The radius is 8, so the circumference is 

\(\displaystyle 8 \cdot 2 \pi = 16 \pi\).

To find the number of which this is 40%, divide this by 40%, or \(\displaystyle \frac{40 }{100}\):

\(\displaystyle 16 \pi \div\frac{40 }{100} = 16 \pi \div\frac{2}{5} = 16 \pi \cdot \frac{5} {2} = \frac{80 \pi} {2} = 40 \pi\)

Corresponding angles of similar triangles are congruent, so 

\(\displaystyle m \angle E = m \angle B = 90 ^{\circ }\)

\(\displaystyle m \angle F = m \angle C = 45 ^{\circ }\)

The degree measures of the angles of a triangle total 180, so

\(\displaystyle m \angle D =180^{\circ } - (m \angle F +m \angle E )\)

\(\displaystyle m \angle D =180^{\circ } - (90^{\circ } +45^{\circ } ) = 45^{\circ }\)

Since \(\displaystyle \angle D\) and \(\displaystyle \angle F\) are congruent, by the Isosceles Triangle Theorem, 

\(\displaystyle \overline{EF} \cong \overline{DE}\)

making \(\displaystyle \bigtriangleup DEF\) isosceles.

The ladder, which is 30 feet long, is the hypotenuse of a right triangle whose legs are the line from the top of the ladder to the ground, which has length \(\displaystyle N\) feet, and the line from the bottom of the ladder horizontally to the house, whose length we will call \(\displaystyle M\) feet. See the diagram below.

By the Pythagorean Theorem,

\(\displaystyle M^{2}+N^{2} = 30 ^{2} = 900\)

Solving for \(\displaystyle M\):

\(\displaystyle M^{2}+N^{2} - N^{2} = 900 - N^{2}\)

\(\displaystyle M^{2}= 900 - N^{2}\)

\(\displaystyle M = \sqrt{900 - N^{2}}\), the correct choice.

To find the area of a perimeter, we add all of the side lengths together. 

\(\displaystyle 9+15+6+8+3+7=48\)

To find the area of a perimeter, we add all of the side lengths together. 

\(\displaystyle 8+7+4+1+4+8=32\)

To find the area of a perimeter, we add all of the side lengths together. 

\(\displaystyle 12+5+8+4+4+9=42\)