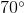Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : HSPT Mathematics

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

What angle is complementary to $65$^{\circ}$$ ?

Possible Answers:

$25$^{\circ}$$

$35$^{\circ}$$

$130$^{\circ}$$

$115$^{\circ}$$

$65$^{\circ}$$

Correct answer:

$25$^{\circ}$$

Explanation:

To find the other angle, subtract the given angle from $90$^{\circ}$$ since complementary angles add up to $90$^{\circ}$$ .

The complementary is:

$\angle 90-\angle65 = \angle25$

Report an Error

Example Question #11 : How To Find The Measure Of An Angle

What is the supplementary angle to $100$^{\circ}$$ ?

Possible Answers:

$280$^{\circ}$$

$80$^{\circ}$$

$10$^{\circ}$$

$170$^{\circ}$$

$70$^{\circ}$$

Correct answer:

$80$^{\circ}$$

Explanation:

Supplementary angles add up to $180$^{\circ}$$ . In order to find the correct angle, take the known angle and subtract that from $180$^{\circ}$$ .

$180$^{\circ}$ -100$^{\circ}$ = 80$^{\circ}$$

Report an Error

Example Question #12 : How To Find The Measure Of An Angle

What angle is complement to $\frac{\pi}{6}$ ?

Possible Answers:

$\frac{\pi}{6}$

$\frac{2\pi}{3}$

$\frac{\pi}{9}$

$\frac{\pi}{4}$

$\frac{\pi}{3}$

Correct answer:

$\frac{\pi}{3}$

Explanation:

The complement to an angle is ninety degrees subtract the angle since two angles must add up to 90. In this case, since we are given the angle in radians, we are subtracting from $\frac{\pi}{2}$ instead to find the complement. The conversion between radians and degrees is: $\pi \textup{ radians } = 180 \textup{ degrees}$

$\frac{\pi}{2}-\frac{\pi}{6}$

Reconvert the fractions to the least common denominator.

$\frac{\pi}{2}-\frac{\pi}{6} = \frac{3\pi}{6}-\frac{\pi}{6} = \frac{2\pi}{6}$

Reduce the fraction.

$\frac{2\pi}{6} = \frac{\pi}{3}$

Report an Error

Example Question #13 : How To Find The Measure Of An Angle

Spinner target 2

The above diagram shows a spinner. The radius of the smaller quarter-circles is half that of the larger quarter-circles.

A player spins the above spinner. What is the probability that the spinner will stop while pointing inside a red region?

Possible Answers:

$\frac{11}{24}$

$\frac{2}{7}$

$\frac{7}{24}$

$\frac{5}{13}$

Correct answer:

$\frac{7}{24}$

Explanation:

The size of the regions does not matter here. What matters is the angle measurement, or, equivalently, what part of a circle each sector is.

The two smaller red regions each comprise one fourth of one fourth of a circle, or

$\frac{1}{4} \times \frac{1}{4} = \frac{1}{16}$ circle.

The two larger red regions each comprise one third of one fourth of a circle, or

$\frac{1}{4} \times \frac{1}{3} = \frac{1}{12}$ circle.

Therefore, the total angle measure comprises

$\frac{1}{16} + \frac{1}{16} + \frac{1}{12} + \frac{1}{12}$

$=\frac{3}{48} + \frac{3}{48} + \frac{4}{48} + \frac{4}{48}$

$= \frac{14}{48} = \frac{7}{24}$

of a circle.

This makes $\frac{7}{24}$ the correct probability.

Report an Error

Example Question #11 : How To Find The Measure Of An Angle

Spinner target 2

The above diagram shows a spinner. The radius of the smaller quarter-circles is half that of the larger quarter-circles.

A player spins the above spinner. What are the odds against the spinner landing while pointing inside one of the blue regions?

Possible Answers:

8 to 5

13 to 11

17 to 7

5 to 2

Correct answer:

17 to 7

Explanation:

The size of the regions does not matter here. What matters is the angle measurement, or, equivalently, what part of a circle each sector is.

Two of the blue sectors are each one third of one quarter-circle, and thus are

$\frac{1}{3} \times \frac{1}{4} = \frac{1}{12}$

of one circle.

The other two blue sectors are each one fourth of one quarter-circle, and thus are

$\frac{1}{4} \times \frac{1}{4} = \frac{1}{16}$

of one circle.

Therefore, the total angle measure comprises

$\frac{1}{16} + \frac{1}{16} + \frac{1}{12} + \frac{1}{12}$

$=\frac{3}{48} + \frac{3}{48} + \frac{4}{48} + \frac{4}{48}$

$= \frac{14}{48} = \frac{7}{24}$

of a circle. This makes $\frac{7}{24}$ the correct probability. As odds, this translates to

(24 -7): 7 , or 17:7 odds against the spinner landing in blue.

Report an Error

Example Question #12 : How To Find The Measure Of An Angle

Spinner target 2

The above diagram shows a spinner. The radius of the smaller quarter-circles is half that of the larger quarter-circles.

A player spins the above spinner. What are the odds against the spinner landing while pointing inside the purple region?

Possible Answers:

13 to 1

11 to 1

7 to 1

9 to 1

Correct answer:

11 to 1

Explanation:

The size of the regions does not matter here. What matters is the angle measurement, or, equivalently, what part of a circle each sector is.

The purple region is one third of one quarter of a circle, or, equvalently,

$\frac{1}{3} \times \frac{1}{4} = \frac{1}{12}$

of a circle, so its central angle is $\frac{1}{12}$ of the total measures of the angles of the sectors. This makes $\frac{1}{12}$ the probability of the spinner stopping inside the purple region; this translates to

(12-1):1 or 11:1 odds against this occurrence.

Report an Error

Example Question #15 : How To Find The Measure Of An Angle

In parallelogram ABCD , $m \angle A = (t+ 56 )^{\circ }$ . Give the measure of $\angle B$ in terms of .

Possible Answers:

$(124-t )^{\circ }$

$(t+ 56 )^{\circ }$

$(34-t )^{\circ }$

$(t+ 146)^{\circ }$

Correct answer:

$(124-t )^{\circ }$

Explanation:

$\angle A$ and $\angle B$ are a pair of adjacent angles of the parallelogram, and as such, they are supplementary - that is, their degree measures total 180. Therefore,

$m \angle A + m \angle B = 180 ^{\circ }$

$m \angle B = 180 ^{\circ } - m \angle A$

$= 180 ^{\circ } - (t+ 56 )^{\circ }$

$= (180 - 56 - t )^{\circ }$

$= (124-t )^{\circ }$

Report an Error

Example Question #16 : How To Find The Measure Of An Angle

The measures of the angles of $\bigtriangleup ABC$ are as follows:

$m \angle A = (3t-14)^{\circ }$

$m \angle B = (2t+16)^{\circ }$

$m \angle C =( 5t)^{\circ }$

Is this triangle acute, obtuse, right, or nonexistent?

Possible Answers:

$\bigtriangleup ABC$ is a right triangle

$\bigtriangleup ABC$ cannot exist

$\bigtriangleup ABC$ is an acute triangle

$\bigtriangleup ABC$ is an obtuse triangle

Correct answer:

$\bigtriangleup ABC$ is an acute triangle

Explanation:

The sum of the measures of the angles of a triangle is 180 degrees, so solve for in the equation:

$m \angle A + m \angle B + m \angle C = 180^{\circ }$

(3t-14) + (2t+16) + 5t = 180

10t+ 2 = 180

10t+ 2- 2 = 180 - 2

10t = 178

$10t \div 10 = 178 \div 10$

t = 17.8

$m \angle A = (3t-14)^{\circ } = (3 \cdot 17.8-14)^{\circ } = (53.4-14)^{\circ } = 39.4^{\circ }$

$m \angle B = (2t+16)^{\circ } = (2 \cdot 17.8 + 16)^{\circ }= (35.6+ 16) ^{\circ }= 51.6^{\circ }$

$m \angle C =( 5t)^{\circ } = ( 5 \cdot 17.8)^{\circ } = 89 ^{\circ }$

All three angles measure less than 90 degrees and are therefore acute angles; that makes $\bigtriangleup ABC$ an acute triangle.

Report an Error

Example Question #221 : Geometry

If you have a right triangle, what is the measure of the two of the angles if they are equal?

Possible Answers:

135

Correct answer:

Explanation:

The total degrees of the angles in a triangle are 180 .

Since it is a right triangle, one of the three angles must be 90.

That leaves you with for the other two angles (180-90=90) .

If they are equal, you just divide the remaining degrees by to get 90/2=45 .

Report an Error

Example Question #11 : How To Find The Measure Of An Angle

If you have a right triangle with an angle measuring 45 degrees, what is the third angle measurement?

Possible Answers:

$90^\circ$

$30^\circ$

$45^\circ$

$180^\circ$

$60^\circ$

Correct answer:

$45^\circ$

Explanation:

A right triangle has one 90 degree angle and all three angles must equal 180 degrees.

To find the answer, just subtract the two angles you have from the total to get

$180^\circ-\textup{Angle 1}-\textup{Angle 2}=\textup{Angle 3}$

The angle we have are,

$\\ \textup{Angle 1}=90^\circ \\ \textup{Angle 2}=45^\circ$ .

Substituting these into the formula results in the solution.

$180^\circ-90^\circ-45^\circ=45^\circ$ .

Report an Error

View Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View Tutors

Meg, M.Ed.
Certified Tutor

The University of Tennessee, Bachelor of Science, Hospitality Administration and Management. Lincoln Memorial University, Mas...

View Tutors

Frank
Certified Tutor

Ursinus College, Bachelor of Science, Mathematics. Lehigh University, Master of Science, Mathematics.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Los Angeles, Chemistry Tutors in Washington DC, LSAT Tutors in San Diego, English Tutors in Boston, GRE Tutors in Denver, ACT Tutors in New York City, GRE Tutors in Atlanta, Calculus Tutors in San Francisco-Bay Area, MCAT Tutors in Houston, GRE Tutors in Miami

Popular Courses & Classes

ISEE Courses & Classes in Washington DC, GRE Courses & Classes in Los Angeles, GRE Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Denver, ACT Courses & Classes in Los Angeles, ISEE Courses & Classes in Chicago, GRE Courses & Classes in San Diego, SSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Chicago, GRE Courses & Classes in Phoenix

Popular Test Prep

SAT Test Prep in Seattle, ISEE Test Prep in Chicago, MCAT Test Prep in Denver, LSAT Test Prep in Houston, MCAT Test Prep in Chicago, SSAT Test Prep in Miami, SSAT Test Prep in Denver, GRE Test Prep in Los Angeles, LSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : HSPT Mathematics

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #1 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

Example Question #11 : How To Find The Measure Of An Angle

Example Question #12 : How To Find The Measure Of An Angle

Example Question #13 : How To Find The Measure Of An Angle

Example Question #11 : How To Find The Measure Of An Angle

Example Question #12 : How To Find The Measure Of An Angle

Example Question #15 : How To Find The Measure Of An Angle

Example Question #16 : How To Find The Measure Of An Angle

Example Question #221 : Geometry

Example Question #11 : How To Find The Measure Of An Angle

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: