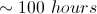The large rectangle has length 80 and width 40, and, consequently, area

.

The white region is a rectangle with length 30 and width 20, and, consequently, area 

.

The white region is 

of the large rectangle.

Each side can be divided into three 3-foot sections.  This gives a total of  squares.  Another way of looking at the problem is that the total area of the large square is 81 and each smaller square has an area of 9.  Dividing 81 by 9 gives the correct answer.

If you answered that the whirlpool’s area is 18.84 feet and therefore fits, you are incorrect because 18.84 is the circumference of the whirlpool, not the area.

If you answered that the area of the whirlpool is 56.52 feet, you multiplied the area of the whirlpool by 1.5 and assumed that that was the correct area, not the legal limit.

If you answered that the area of the backyard was smaller than the area of the whirlpool, you did not calculate area correctly.

And if you thought the area of the backyard was 30 feet, you found the perimeter of the backyard, not the area.

The correct answer is that the area of the whirlpool is 28.26 feet and, when multiplied by 1.5 = 42.39, which is smaller than the area of the backyard, which is 56 square feet. 

Using the Pythagorean Theorem, the diameter of the circle (also the diagonal of the square) can be found to be 4√2.  Thus, the radius of the circle is half of the diameter, or 2√2.  The area of the circle is then π(2√2)², which equals 8π.  Next, the area of the square must be subtracted from the entire circle, yielding an area of 8π-16 square inches.

The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.)  Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 88 inches for our problem. Its total area would be 88 * 88 or 7744 in².

 Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr² or π * 44² = 1936π in². Therefore, the area remaining would be 7744 – 1936π. The cost of the waste would be 0.25 * (7744 – 1936π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 4 from our subtraction. This would give us: 0.25 * 4 * (1936 – 484π). Since 0.25 is equal to 1/4, 0.25 * 4 = 1. Therefore, our final answer is: 1936 – 484π dollars.

The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 50 inches for our problem. Its total area would be 50 * 50 or 2500 in².

Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr² or π * 25² = 625π in². Therefore, the area remaining would be 2500 - 625π. The cost of the waste would be 0.2 * (2500 – 625π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 5 from our subtraction. This would give us: 0.2 * 5 * (500 – 125π). Since 0.2 is equal to 1/5, 0.2 * 625 = 125. Therefore, our final answer is: 500 – 125π dollars.

First we will calculate the total area of the placemat:

Next we will calculate the area of the circular place

And

So

We will subtract the area of the plate from the total area

Allen has been running for 10 minutes since he lost his keys at 3m/s.  This gives us a maximum distance of  from his current location.  If we move 1800m in all directions, this gives us a circle with radius of 1800m.  The area of this circle is

Our answer, however, is asked for in kilometers.  1800m=1.8km, so our actual area will be  square kilometers.  Since he can search 1 per hour, it will take him at most 10.2 hours to find his keys.

The area of a square is:

Substitute the length and simplify.

A square with area 64 has as the length of one of its sides the square root of this area, which is . The length of a diagonal of a square is  times this sidelength, so the square has diagonals of length .

25% of this is

.