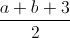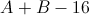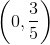We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : HSPT Mathematics

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 … 204 205 206 207 208 209 210 211 212 213 214 215 Next →

Example Question #2071 : Hspt Mathematics

Axes

Give the equation of the red line in slope-intercept form.

Possible Answers:

$y = -\frac{4}{7}x + 6$

$y = \frac{4}{7}x + 6$

$y =- \frac{7}{4}\left (x + 6 \right )$

$y = \frac{7}{4}x + 6$

$y =- \frac{7}{4}x + 6$

Correct answer:

$y = \frac{7}{4}x + 6$

Explanation:

The slope of the line is

$m = \frac{y_{2}- y_{1}}{x_{2}- x_{1}} = \frac{6- (-1)}{0-(-4)} = \frac{7}{4}$

The -intercept of the line has -coordinate b= 6

The slope-intercept form can be written:

y = mx+b

Replace:

$y = \frac{7}{4}x+6$

Report an Error

Example Question #2071 : Hspt Mathematics

Axes_2

The green and blue lines are perpendicular: What is the slope of the blue line?

Possible Answers:

$\frac{1}{3}$

It cannot be determined from the information given.

$-\frac{1}{3}$

Correct answer:

Explanation:

The slope of the blue line, being perpendicular to the green line, is the opposite of the reciprocal of the slope of the green line. The slope of the green line can be found using the slope formula:

$m = \frac{y_{2}- y_{1}}{x_{2}- x_{1}} = \frac{10-0}{0-30} = -\frac{1}{3}$

The opposite of the reciprocal of $-\frac{1}{3}$ is 3, and this is the slope of the blue line.

Report an Error

Example Question #1 : How To Find The Midpoint Of A Line Segment

A line segment on the coordinate plane has endpoints (a-5,-b) and (b+8, a-4) . In terms of and , as applicable, give the -coordinate of its midpoint.

Possible Answers:

$\frac{a + b + 3}{2}$

a - b - 4

a + b + 3

$\frac{a - b - 4}{2}$

$\frac{a - b - 13}{2}$

Correct answer:

$\frac{a + b + 3}{2}$

Explanation:

The -coordinate of the midpoint of a line segment is the mean of the -coordinates of its endpoints. Therefore, the -coordinate is

$x= \frac{(a-5)+(b+8)}{2} = \frac{a+b-5+8}{2} = \frac{a+b+3}{2}$ .

Report an Error

Example Question #1 : Midpoint Formula

A line segment on the coordinate plane has endpoints (a-5,-b) and (b+8, a-4) . In terms of and , as applicable, give the -coordinate of its midpoint.

Possible Answers:

$\frac{a + b + 3}{2}$

$\frac{a + b - 4}{2}$

a + b + 3

$\frac{a - b - 4}{2}$

a - b - 4

Correct answer:

$\frac{a - b - 4}{2}$

Explanation:

The -coordinate of the midpoint of a line segment is the mean of the -coordinates of its endpoints. Therefore, the -coordinate is

$y= \frac{(a-4)+(-b)}{2} = \frac{a-b-4}{2}$ .

Report an Error

Example Question #1 : Midpoint Formula

A line segment on the coordinate plane has midpoint $\left ( A + 5, B + 7\right )$ . One of its endpoints is $\left ( 10, 6 \right )$ . What is the -coordinate of the other endpoint, in terms of and/or ?

Possible Answers:

2B + 1

2B + 8

B + 8

B + 1

2B + 20

Correct answer:

2B + 8

Explanation:

Let be the -coordinate of the other endpoint. Since the -coordinate of the midpoint of the segment is the mean of those of the endpoints, we can set up an equation as follows:

$\frac{Y + 6 }{2} = B + 7$

$\frac{Y + 6 }{2} \cdot 2= \left ( B + 7 \right )\cdot 2$

Y + 6 = 2B + 14

Y + 6 -6 = 2B + 14 -6

Y = 2B + 8

Report an Error

Example Question #2 : How To Find The Endpoints Of A Line Segment

A line segment on the coordinate plane has one endpoint at $\left ( 8, 10 \right )$ ; its midpoint is $\left ( A+B, A- B\right )$ . Which of the following gives the -coordinate of its other endpoint in terms of and ?

Possible Answers:

A + B- 8

A + B- 16

2 A + 2B- 8

2 A + 2B+8

A + B+8

Correct answer:

2 A + 2B- 8

Explanation:

To find the value of the -coordinate of the other endpoint, we will assign the variable . Then, since the -coordinate of the midpoint of the segment is the mean of those of its endpoints, the equation that we can set up is

$\frac{T + 8 }{2} = A + B$ .

We solve for :

$\frac{T + 8 }{2} \cdot 2 =\left ( A + B \right )\cdot 2$

T + 8 =2 A + 2B

T + 8 - 8 =2 A + 2B- 8

T =2 A + 2B- 8

Report an Error

Example Question #291 : Geometry

Two perpendicular lines intersect at the point (5,4) . One line passes through point (3,1) ; the other passes through point $\left ( 4, Y\right )$ . Evaluate .

Possible Answers:

$Y =- 2\frac{1}{2}$

$Y = 2\frac{1}{2}$

$Y = 3\frac{1}{3}$

$Y = 4\frac{2}{3}$

$Y = 5\frac{1}{2}$

Correct answer:

$Y = 4\frac{2}{3}$

Explanation:

The line that passes through $\left ( 3,1\right )$ and $\left ( 5,4\right )$ has slope

$m = \frac{4-1}{5-3} = \frac{3}{2}$ .

The line that passes through $\left ( 4, Y\right )$ and (5,4) , being perpendicular to the first, has as its slope the opposite reciprocal of $\frac{3}{2}$ , or $-\frac{2}{3}$ .

Therefore, to find , we use the slope formula and solve for :

$-\frac{2}{3} = \frac{Y-4}{4-5}$

$-\frac{2}{3} = \frac{Y-4}{-1}$

$-\frac{2}{3} \cdot (-1) = \frac{Y-4}{-1} \cdot (-1)$

$\frac{2}{3}= Y-4$

$\frac{2}{3}+ 4= Y-4 + 4$

$4\frac{2}{3}= Y$

Report an Error

Example Question #1 : How To Find X Or Y Intercept

What is the -intercept of the graph of the function $f \left ( x\right ) = 2x^{2} - 7x + 5$ ?

Possible Answers:

$\left (0,5 \right )$

$\left (0,0 \right )$

$\left (0,2 \right )$

$\left ( 0, -3 \frac{1}{2}\right )$

$\left (0,-7 \right )$

Correct answer:

$\left (0,5 \right )$

Explanation:

The -intercept of the graph of a function is the point at which it intersects the -axis - that is, at which x = 0 . This point is $\left (0, f(0) \right )$ , so evaluate f(0) :

$f \left ( x\right ) = 2x^{2} - 7x + 5$

$f \left (0\right ) = 2 \cdot 0^{2} - 7 \cdot 0 + 5$

$f \left (0\right ) = 0- 0 + 5 = 5$

The -intercept is $\left (0,5 \right )$ .

Report an Error

Example Question #4 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6

Give the -intercept, if there is one, of the graph of the equation

$y = \frac{1}{x^{2}+ x} + 3$

Possible Answers:

$\left ( 0, \frac{3}{2}\right )$

(0,3)

The graph has no -intercept.

(0,2)

(0,4)

Correct answer:

The graph has no -intercept.

Explanation:

The -intercept is the point at which the graph crosses the -axis; at this point, the -coordinate is 0, so substitute for in the equation:

$y = \frac{1}{x^{2}+ x} + 3$

$y = \frac{1}{0^{2}+0} + 3$

$y = \frac{1}{0} + 3$

However, since this expression has 0 in a denominator, it is of undefined value. This means that there is no value of paired with -coordinate 0, and, subsequently, the graph of the equation has no -intercept.

Report an Error

Example Question #5 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6

Give the -intercept, if there is one, of the graph of the equation

$y = \frac{3}{\left | 3x-8\right |}$

Possible Answers:

$\left ( 0, \frac{3}{8}\right )$

The graph has no -intercept.

$\left ( 0, \frac{3}{5}\right )$

$\left ( 0,- \frac{3}{5}\right )$

$\left ( 0, -\frac{3}{8}\right )$

Correct answer:

$\left ( 0, \frac{3}{8}\right )$

Explanation:

The -intercept is the point at which the graph crosses the -axis; at this point, the -coordinate is 0, so substitute for in the equation:

$y = \frac{3}{\left | 3x-8\right |}$

$y = \frac{3}{\left | 3 \cdot 0 -8\right |}$

$y = \frac{3}{\left | 0 -8\right |}$

$y = \frac{3}{\left | -8\right |}$

$y = \frac{3}{ 8}$

The -intercept is $\left ( 0, \frac{3}{8}\right )$ .

Report an Error

← Previous 1 2 … 204 205 206 207 208 209 210 211 212 213 214 215 Next →

View Tutors

Swagatika
Certified Tutor

Regional Institute of Education Bhubaneswar, Bachelor of Economics, Mathematics.

View Tutors

Stephen
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor of Science, Geophysics and Seismology.

View Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Boston, SAT Tutors in Miami, Algebra Tutors in Houston, Statistics Tutors in Denver, ISEE Tutors in Phoenix, Computer Science Tutors in San Francisco-Bay Area, GMAT Tutors in Houston, Math Tutors in Los Angeles, MCAT Tutors in Atlanta, Statistics Tutors in Philadelphia

Popular Courses & Classes

GMAT Courses & Classes in Houston, ACT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Washington DC, ACT Courses & Classes in San Diego, GRE Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in San Diego, LSAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Boston, GRE Courses & Classes in Philadelphia, ISEE Courses & Classes in Los Angeles

Popular Test Prep

ISEE Test Prep in San Francisco-Bay Area, ACT Test Prep in Boston, ACT Test Prep in San Diego, GRE Test Prep in San Francisco-Bay Area, GMAT Test Prep in Boston, GMAT Test Prep in Chicago, LSAT Test Prep in New York City, ISEE Test Prep in Philadelphia, SAT Test Prep in Washington DC, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : HSPT Mathematics

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #2071 : Hspt Mathematics

Example Question #2071 : Hspt Mathematics

Example Question #1 : How To Find The Midpoint Of A Line Segment

Example Question #1 : Midpoint Formula

Example Question #1 : Midpoint Formula

Example Question #2 : How To Find The Endpoints Of A Line Segment

Example Question #291 : Geometry

Example Question #1 : How To Find X Or Y Intercept

Example Question #4 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6

Example Question #5 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: