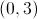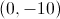Apply the distance formula, substituting the -coordinates for  and  and the -coordinates for  and :

A line perpendicular to a line with slope has as its slope the opposite of the reciprocal of ; this number is . The line passes through the origin, which is the point ; this is also the -intercept. In slope-intercept form, its equation can be found by substituting in the equation:

This can be rewritten in standard form as follows:

The origin is . In the following slope formula, set

,

and solve for :

 and  are represented by a horizontal line and a vertical line, respectively; therefore, their graphs are perpendicular.

As for the third equation, , this is represented by a line with slope , as seen below:

The equation is in slope-intercept form, and the slope of the line is the coefficient of , which is . It is perpendicular to a line with slope ; however, the horizontal line has slope 0, and the vertical line has undefined slope. 

The correct choice is therefore I and II.

Since you move right  units in the second step and right  units in the fourth, you will move a total of  units right; this means the -coordinate will be , which is equal to 72.

Since you move up  units in the first step and down  units in the third, you will move a total of  units up; this means the -coordinate will be , which is equal to 46.

We can form a system of equations and solve by adding, as follows:

The -intercept of the graph of a function is the point at which it intersects the -axis - that is, at which . This point is , so evaluate :

The -intercept is .

The lateral area (not including its bases) is equal to the circumference of the base times the height of the cylinder. Think of it like a label that is wrapped around a soup can. Therefore, we can write this area as:

A = h * π * d or A = h * π * 2r = 2πrh

Now, substituting in our values, we get:

512.5π = 2 * 41*rπ; 512.5π = 82rπ

Solve for r by dividing both sides by 82π:

6.25 = r

From here, we can calculate the area of a base:

A = 6.25²π = 39.0625π

NOTE: The question asks for the area of the bases. Therefore, the answer is 2 * 39.0625π or 78.125π in².

We need to find expressions for the surface area and the volume of a cylinder. The surface area of the cylinder consists of the sum of the surface areas of the two bases plus the lateral surface area.

surface area of cylinder = surface area of bases + lateral surface area

The bases of the cylinder will be two circles with radius r. Thus, the area of each will be πr², and their combined surface area will be 2πr².

The lateral surface area of the cylinder is equal to the circumference of the circular base multiplied by the height. The circumferece of a circle is 2πr, and the height is h, so the lateral area is 2πrh.

surface area of cylinder = 2πr² + 2πrh

Next, we need to find an expression for the volume. The volume of a cylinder is equal to the product of the height and the area of one of the bases. The area of the base is πr², and the height is h, so the volume of the cylinder is πr²h.

volume = πr²h

Then, we must set the volume and surface area expressions equal to one another and solve for r in terms of h.

2πr² + 2πrh = πr²h

First, let's factor out 2πr from the left side.

2πr(r + h) = πr²h

We can divide both sides by π.

2r(r + h) = r²h

We can also divide both sides by r, because the radius cannot equal zero.

2(r + h) = rh

Let's now distribute the 2 on the left side.

2r + 2h = rh

Subtract 2r from both sides to get all the r's on one side.

2h = rh – 2r

rh – 2r = 2h 

Factor out an r from the left side.

r(h – 2) = 2h

Divide both sides by h – 2

r = 2h/(h – 2)

The answer is r = 2h/(h – 2).

When you're calculating the surface area of a cylinder, note that the cylinder will have two circles, one for the top and one for the bottom, and one rectangle that wraps around the "side" of the cylinder (it's helpful to picture peeling the label off a can of soup - it's curved when it's on the can, but really it's a rectangle that has been wrapped around).  You know the area of the circle formula; for the rectangle, note that the height is given to you but the width of the rectangle is one you have to intuit: it's the circumference of the circle, because the entire distance around the circle from one point around and back again is the horizontal distance that the area must cover.

Therefore the surface area of a cylinder = 

This problem is relatively simple. We know that the volume of a cube is equal to s³, where s is the length of a given side of the cube. Therefore, to find our dimensions, we merely have to solve s³ = 1728. Taking the cubed root, we get s = 12.

Since the sides of a cube are all the same, the surface area of the cube is equal to 6 times the area of one face. For our dimensions, one face has an area of 12 * 12 or 144 in². Therefore, the total surface area is 6 * 144 = 864 in².