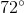HSPT Math : HSPT Mathematics
Study concepts, example questions & explanations for HSPT Math
All HSPT Math Resources
Example Questions
Example Question #1 : How To Find An Angle In A Trapezoid
Find the measure of angle 
The sum of the angles in any quadrilateral is 360°, and the properties of an isosceles trapezoid dictate that the sets of angles adjoined by parallel lines (in this case, the bottom set and top set of angles) are equal. Subtracting 2(72°) from 360° gives the sum of the two top angles, and dividing the resulting 216° by 2 yields the measurement of x, which is 108°.
Example Question #2 : Acute / Obtuse Triangles
Two interior angles in an obtuse triangle measure 
Interior angles of a triangle always add up to 180 degrees.
Example Question #1 : Acute / Obtuse Triangles
In the triangle below, AB=BC (figure is not to scale) . If angle A is 41°, what is the measure of angle B?
A (Angle A = 41°)
B C
41
98
90
82
98
If angle A is 41°, then angle C must also be 41°, since AB=BC. So, the sum of these 2 angles is:
41° + 41° = 82°
Since the sum of the angles in a triangle is 180°, you can find out the measure of the remaining angle by subtracting 82 from 180:
180° - 82° = 98°
Example Question #21 : Acute / Obtuse Triangles
Points A, B, C, D are collinear. The measure of ∠ DCE is 130° and of ∠ AEC is 80°. Find the measure of ∠ EAD.
60°
80°
70°
50°
50°
To solve this question, you need to remember that the sum of the angles in a triangle is 180°. You also need to remember supplementary angles. If you know what ∠ DCE is, you also know what ∠ ECA is. Hence you know two angles of the triangle, 180°-80°-50°= 50°.
Example Question #2 : Acute / Obtuse Triangles
Points A, B, and C are collinear (they lie along the same line). The measure of angle CAD is 
Find the measure of 
The measure of 
Because the measures of the three angles in a triangle must add up to 
Example Question #1 : Triangles
Points A and B lie on a circle centered at Z, where central angle <AZB measures 140°. What is the measure of angle <ZAB?
15°
30°
Cannot be determined from the given information
20°
25°
20°
Because line segments ZA and ZB are radii of the circle, they must have the same length. That makes triangle ABZ an isosceles triangle, with <ZAB and <ZBA having the same measure. Because the three angles of a triangle must sum to 180°, you can express this in the equation:
140 + 2x = 180 --> 2x = 40 --> x = 20
Example Question #1 : Triangles
Triangle FGH has equal lengths for FG and GH; what is the measure of ∠F, if ∠G measures 40 degrees?
40 degrees
100 degrees
70 degrees
None of the other answers
140 degrees
70 degrees
It's good to draw a diagram for this; we know that it's an isosceles triangle; remember that the angles of a triangle total 180 degrees.
Angle G for this triangle is the one angle that doesn't correspond to an equal side of the isosceles triangle (opposite side to the angle), so that means ∠F = ∠H, and that ∠F + ∠H + 40 = 180,
By substitution we find that ∠F * 2 = 140 and angle F = 70 degrees.
Example Question #163 : Triangles
The vertex angle of an isosceles triangle is 
An isosceles triangle has two congruent base angles and one vertex angle. Each triangle contains 
Example Question #164 : Triangles
In an isosceles triangle the base angle is five less than twice the vertex angle. What is the sum of the vertex angle and the base angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 
and 
So the equation to solve becomes
or
Thus the vertex angle is 38 and the base angle is 71 and their sum is 109.
Example Question #2 : Triangles
Sides 
This triangle has an angle of 
All HSPT Math Resources
