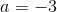We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #545 : Algebra

Solve: $-\frac{6}{x}+1 = 5$

Possible Answers:

$\frac{2}{3}$

$-\frac{3}{2}$

Correct answer:

$-\frac{3}{2}$

Explanation:

To isolate the variable, first subtract one from both sides of the equation.

$-\frac{6}{x}+1 -(1)= 5-(1)$

$-\frac{6}{x} = 4$

Multiply by negative on both sides of the equation.

6=-4x

Divide by four on both sides of the equation and reduce.

$x=-\frac{6}{4}=-\frac{3}{2}$

Report an Error

Example Question #546 : Algebra

Solve: -6x+7 = -11

Possible Answers:

$\frac{11}{42}$

$-\frac{2}{3}$

$\frac{2}{3}$

Correct answer:

Explanation:

The goal is to isolate the unknown variable.

Subtract from both sides of the equation.

-6x+7 -(7)= -11-(7)

-6x = -18

Divide by on both sides.

$x=\frac{-18}{-6} = 3$

Report an Error

Example Question #1754 : Hspt Mathematics

Evaluate: $-\frac{2}{z} =-8$

Possible Answers:

$\frac{1}{10}$

$\frac{1}{4}$

$\frac{1}{16}$

Correct answer:

$\frac{1}{4}$

Explanation:

To solve this problem, isolate the variable.

Multiply by on both sides of the equation to eliminate the fraction and negative sign.

$-\frac{2}{z} \times (-z)=-8\times( -z)$

2=8z

Divide both sides by .

$z=\frac{2}{8}=\frac{1}{4}$

Report an Error

Example Question #1162 : Concepts

Solve the following equation: 3x-3 = 18

Possible Answers:

Correct answer:

Explanation:

In order to isolate the unknown variable, first add three from both sides of the equation to move the negative three to the right side of the equation.

3x-3 +(3)= 18+(3)

Simplify the left and right sides.

3x=21

Divide by three on both sides.

$\frac{3x}{3}=\frac{21}{3}$

Simplify the left and right sides.

x=7

Report an Error

Example Question #1161 : Concepts

Solve the following for :

3x-4=11

Possible Answers:

$\frac{7}{3}$

Correct answer:

Explanation:

To solve for a particular variable, you must isolate the variable on one side of the equation and all other constants on the other side. To do this, perform the opposite operation to manipulate the equation.

To solve, you must isolate x by first adding 4 to both sides adn then dividing by 3.

Thus,

$3x-4+4=11+4\Rightarrow 3x=15\Rightarrow \frac{3x}{3}=\frac{15}{3}\Rightarrow x=5$

Report an Error

Example Question #1 : Solve Multi Step Problems With Positive And Negative Rational Numbers: Ccss.Math.Content.7.Ee.B.3

Define an operation $\bigstar$ on the set of real numbers as follows:

$a \bigstar b = a^{2}+ b$

If $6 \bigstar b = 100$ , then what is ?

Possible Answers:

$\sqrt{94}$

$\sqrt{106}$

Correct answer:

Explanation:

$a \bigstar b = a^{2}+ b$ ,

$6 \bigstar b = 6 ^{2} + b = 36 + b$ .

$6 \bigstar b = 100$

then

36 + b= 100

36+ b - 36 = 100 - 36

b = 64

Report an Error

Example Question #2 : Solve Multi Step Problems With Positive And Negative Rational Numbers: Ccss.Math.Content.7.Ee.B.3

Define an operation $\bigstar$ on the set of real numbers as follows:

$a \bigstar b = \frac{a+b}{ab}$ .

If $a \bigstar \frac{1}{2} = -1$ , evaluate .

Possible Answers:

$a = \frac{1}{3}$

a = -3

a = 3

$a = - \frac{1}{3}$

Correct answer:

$a = - \frac{1}{3}$

Explanation:

$a \bigstar b = \frac{a+b}{ab}$

$a \bigstar \frac{1}{2} = \frac{a+ \frac{1}{2} }{a \cdot \frac{1}{2} } = \frac{\frac{2a}{2}+ \frac{1}{2} }{ \frac{a}{2} } = \frac{\frac{2a+1}{2} }{ \frac{a}{2} }$

Equivalently

$a \bigstar \frac{1}{2} = \frac{2a+1}{2} \div \frac{a}{2} = \frac{2a+1}{2} \cdot \frac{2}{a} = \frac{2a+1}{a}$

$a \bigstar \frac{1}{2} = -1$ , so set this equal to :

$\frac{2a+1}{a} = -1$

$\frac{2a+1}{a} \cdot a = -1 \cdot a$

2a+1 = -a

2a+1 + a - 1 = -a + a - 1

3a= - 1

$3a\div 3 = - 1 \div 3$

$a = - \frac{1}{3}$

Report an Error

Example Question #3 : Solve Multi Step Problems With Positive And Negative Rational Numbers: Ccss.Math.Content.7.Ee.B.3

Define an operation $\bigstar$ on the set of real numbers as follows:

$a \bigstar b = \frac{a+b}{ab}$ .

If $a \bigstar 0.5 = 0.1$ , then evaluate .

Possible Answers:

$a = \frac{ 19} {10}$

$a = - \frac{10}{19}$

$a = - \frac{ 19} {10}$

$a = \frac{10}{19}$

Correct answer:

$a = - \frac{10}{19}$

Explanation:

$a \bigstar b = \frac{a+b}{ab}$ ,

$a \bigstar 0.5 = \frac{a+0.5 }{a \cdot 0.5 } = \frac{a+0.5 }{0.5a }$

Set this equal to 0.1:

$\frac{a+0.5 }{0.5a } = 0.1$

$\frac{a+0.5 }{0.5a } \cdot 0.5 a = 0.1 \cdot 0.5 a$

a+0.5 = 0.05 a

$(a+0.5) \cdot 100 = 0.05 a \cdot 100$

$a \cdot 100 +0.5 \cdot 100 = 5 a$

100a +5 0= 5 a

100a +50 - 100a = 5 a - 100a

50 = -95a

$50 \div (-95) = -95a \div (-95)$

$a = -\frac{50}{95} = - \frac{10}{19}$

Report an Error

Example Question #1166 : Concepts

is a number less than 36.

Which of the following gives a solution of the equation

|x- 17 | + K = 36

in terms of ?

Possible Answers:

x = -53 - K

x = 19 - K

x = 53 - K

x = -19 - K

Correct answer:

x = 53 - K

Explanation:

|x- 17 | + K = 36 ,

|x- 17 | + K - K = 36 - K

|x- 17 | = 36 - K

Since K < 36 , 36 - K > 0 , so solutions exist. One of the following two situations occurs:

x- 17 = 36 - K

x- 17 + 17 = 36 - K + 17

x = 53 - K

-(x- 17 )= 36 - K

-x+ 17 = 36 - K

-x+ 17 - 17 = 36 - K - 17

-x = 19 - K

-(-x )= -(19 - K)

x = K - 19

Of these two, only x = 53 - K is among the choices, so it is the correct choice.

Report an Error

Example Question #1164 : Concepts

If L < 32 , then which of the following is equivalent to the expression | L - 32 | + 12 ?

Possible Answers:

20+L

44 + L

44 - L

20-L

Correct answer:

44 - L

Explanation:

If L < 32 , then L - 32 < 0 , so

| L - 32 | + 12

= -(L - 32 )+ 12

= - L + 32 + 12

= - L + 44

= 44 - L

Report an Error

View Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View Tutors

Kara
Certified Tutor

University of Central Missouri, Bachelor of Science, Science Teacher Education. University of Central Missouri, Certificate, ...

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Atlanta, SAT Tutors in Seattle, Reading Tutors in San Francisco-Bay Area, French Tutors in Denver, ISEE Tutors in San Diego, Statistics Tutors in Washington DC, Reading Tutors in Chicago, French Tutors in San Francisco-Bay Area, Spanish Tutors in Chicago, ACT Tutors in Miami

Popular Courses & Classes

MCAT Courses & Classes in Washington DC, Spanish Courses & Classes in Phoenix, GRE Courses & Classes in Los Angeles, Spanish Courses & Classes in Houston, ISEE Courses & Classes in Miami, SAT Courses & Classes in Chicago, SSAT Courses & Classes in Denver, Spanish Courses & Classes in Denver, LSAT Courses & Classes in Denver, SSAT Courses & Classes in Chicago

Popular Test Prep

LSAT Test Prep in Atlanta, SAT Test Prep in Seattle, SAT Test Prep in Denver, LSAT Test Prep in Boston, SSAT Test Prep in Miami, SSAT Test Prep in Washington DC, LSAT Test Prep in San Diego, LSAT Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #545 : Algebra

Example Question #546 : Algebra

Example Question #1754 : Hspt Mathematics

Example Question #1162 : Concepts

Example Question #1161 : Concepts

Example Question #1 : Solve Multi Step Problems With Positive And Negative Rational Numbers: Ccss.Math.Content.7.Ee.B.3

Example Question #2 : Solve Multi Step Problems With Positive And Negative Rational Numbers: Ccss.Math.Content.7.Ee.B.3

Example Question #3 : Solve Multi Step Problems With Positive And Negative Rational Numbers: Ccss.Math.Content.7.Ee.B.3

Example Question #1166 : Concepts

Example Question #1164 : Concepts

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: