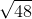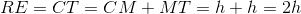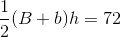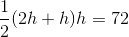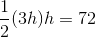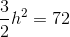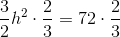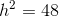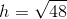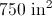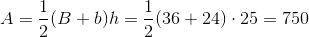Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Geometry

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Triangles

The hypotenuse of a right triangle is feet; it has one leg feet long. Give its area in square inches.

Possible Answers:

$38,880 \textrm{ in}^{2}$

$43,120 \textrm{ in}^{2}$

$42,120 \textrm{ in}^{2}$

$77,760 \textrm{ in}^{2}$

$101,088 \textrm{ in}^{2}$

Correct answer:

$38,880 \textrm{ in}^{2}$

Explanation:

The area of a right triangle is half the product of the lengths of its legs, so we need to use the Pythagorean Theorem to find the length of the other leg. Set c = 39 , b = 36 :

$a^{2} = c^{2} - b^{2}$

$a^{2} = 39 ^{2} - 36^{2}$

$a^{2} = 1,521 - 1,296$

$a^{2} = 225$

$a = \sqrt{225} = 15$

The legs have length and feet; multiply both dimensions by to convert to inches:

$15 \times 12 = 180$ inches

$36 \times 12 = 432$ inches.

Now find half the product:

$A = \frac{1}{2} \cdot 180 \cdot 432 = 38,880\ in^{2}$

Report an Error

Example Question #161 : Geometry

Which of the following is equal to the area of a rectangle with length 4.3 meters and width 3.5 meters?

Possible Answers:

$15,500 \textrm{ cm}^{2}$

$155,000 \textrm{ cm}^{2}$

$15,050 \textrm{ cm}^{2}$

$150,500 \textrm{ cm}^{2}$

Correct answer:

$150,500 \textrm{ cm}^{2}$

Explanation:

Multiply each dimension by 100 to convert meters to centimeters:

$4.3 \times 100 = 430$

$3.5 \times 100 = 350$

Multiply these dimensions to get the area of the rectangle in square centimeters:

$430 \times 350 = 150,500\textrm{ cm}^{2}$

Report an Error

Example Question #1 : How To Find The Area Of A Trapezoid

Trapezoid

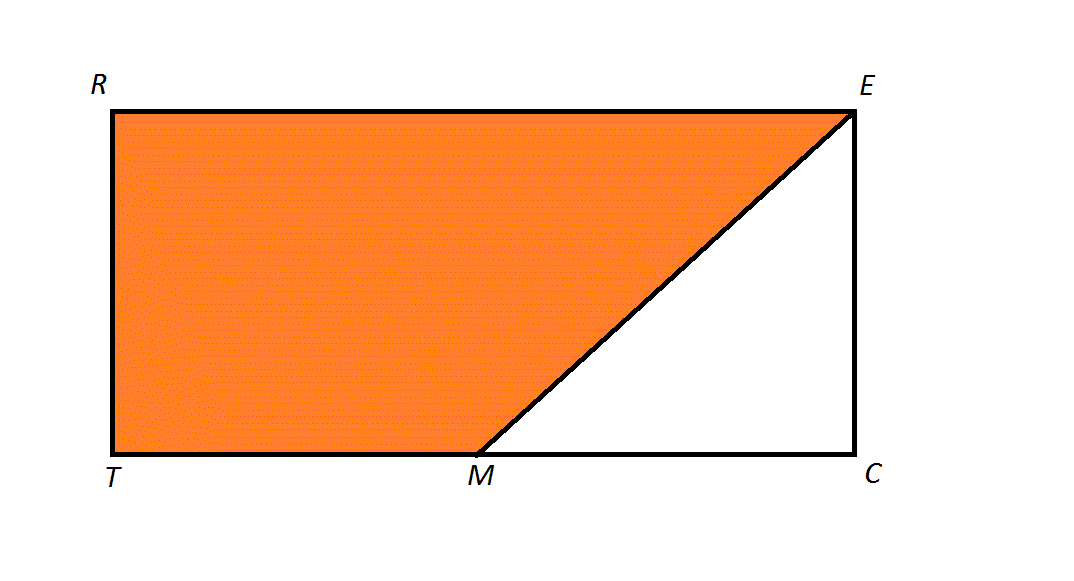
The above diagram depicts a rectangle RECT with isosceles triangle $\Delta ECM$ . If is the midpoint of $\overline{CT}$ , and the area of the orange region is , then what is the length of one leg of $\Delta ECM$ ?

Possible Answers:

$\sqrt {108}$

$\sqrt {48}$

$\sqrt {54}$

$\sqrt {96}$

Correct answer:

$\sqrt {48}$

Explanation:

The length of a leg of $\Delta ECM$ is equal to the height of the orange region, which is a trapezoid. Call this length/height .

Since the triangle is isosceles, then CM = h , and since is the midpoint of $\overline{CT}$ , MT = h . Also, since opposite sides of a rectangle are congruent,

RE = CT = CM + MT = h + h = 2h

Therefore, the orange region is a trapezoid with bases and and height . Its area is 72, so we can set up and solve this equation using the area formula for a trapezoid:

$\frac{1}{2} (B + b)h = 72$

$\frac{1}{2} (2h + h)h = 72$

$\frac{1}{2} (3h )h = 72$

$\frac{3}{2}h^{2} = 72$

$\frac{3}{2}h^{2} \cdot \frac{2}{3} = 72 \cdot \frac{2}{3}$

$h^{2}= 48$

$h = \sqrt {48}$

This is the length of one leg of the triangle.

Report an Error

Example Question #2 : How To Find The Area Of A Trapezoid

A trapezoid has a height of inches and bases measuring inches and inches. What is its area?

Possible Answers:

$600\; \textrm{in}^{2}$

$1,500\; \textrm{in}^{2}$

$750\; \textrm{in}^{2}$

$900\; \textrm{in}^{2}$

$864\; \textrm{in}^{2}$

Correct answer:

$750\; \textrm{in}^{2}$

Explanation:

Use the following formula, with B = 36,b = 24,h=25 :

$A = \frac{1}{2} (B+b)h = \frac{1}{2} (36+24) \cdot 25 = 750$

Report an Error

Example Question #101 : Geometry

What is the area of a triangle with a base of and a height of ?

Possible Answers:

Correct answer:

Explanation:

The formula for the area of a triangle is $\dpi{100} Area=\frac{1}{2}\times base\times height$ .

Plug the given values into the formula to solve:

$\dpi{100} Area=\frac{1}{2}\times 12\times 3$

$\dpi{100} Area=\frac{1}{2}\times 36$

$\dpi{100} Area=18$

Report an Error

Example Question #51 : Geometry

Find the area of a square with side length 1.

Possible Answers:

Correct answer:

Explanation:

To solve, simply use the formula for the area of a square. Thus,

A=s^2=1^2=1

Report an Error

Example Question #52 : Geometry

Find the area of a triangle with height 6 and base 3.

Possible Answers:

Correct answer:

Explanation:

To solve, simply use the formula for the area of a triangle.

Given the height is 6 and the base is 3, substitute these values into area of a triangle formula.

Thus,

$A=\frac{1}{2}Bh=\frac{1}{2}*6*3=9$

Report an Error

Example Question #53 : Geometry

Square a

What is 60% of the area of the above square?

Possible Answers:

$\frac{96}{5} \sqrt{2}$

$19\frac{1}{5}$

$\frac{48}{5} \sqrt{2}$

$38\frac{2}{5}$

Correct answer:

$19\frac{1}{5}$

Explanation:

The area of a square, it being a rhombus, is the product of the lengths of its diagonals. The diagonals are of the same length, so both diagonals have length 8, and the area of the square is

$\frac{1}{2} \times 8^{2} = \frac{1}{2} \times 8 \times 8 = 32$ .

60% of 32 is equal to 32 multiplied by $\frac{60}{100}$ , which is

$32 \times \frac{60}{100} = 32 \times \frac{3}{5} = 19\frac{1}{5}$ .

Report an Error

Example Question #54 : Geometry

A circle has radius 12. Which of the following gives 40% of the area of this circle?

Possible Answers:

$\frac{576 \pi}{5}$

$\frac{144 \pi}{5}$

$\frac{288 \pi}{5}$

$\frac{72 \pi}{5}$

Correct answer:

$\frac{288 \pi}{5}$

Explanation:

The area of a circle with radius is

$A = \pi r^{2}$ .

The radius of the circle is r=12 , so the area is

$A = \pi \cdot 12^{2} = 144 \pi$ .

40% of this is

$144 \pi \cdot \frac{40}{100} = 144 \pi \cdot \frac{2}{5 }= \frac{288 \pi}{5}$

Report an Error

Example Question #53 : Geometry

A rectangle measures six feet in width and four and one-half feet in height. Give its area in square yards.

Possible Answers:

9 square yards

3 square yards

243 square yards

81 square yards

Correct answer:

3 square yards

Explanation:

Convert each dimension from feet to yards by dividing by conversion factor 3:

$6 \textup{ ft} \div 3 \textup{ yd/ft} = 2 \textup{ yd}$

$4 \frac{1}{2} \textup{ ft} \div 3 \textup{ yd/ft} = \frac{9}{2} \textup{ ft} \div 3 \textup{ yd/ft}= \frac{3}{2} \textup{ yd}$

Their product is the area in square yards:

$2 \textup{ yd} \times \frac{3}{2} \textup{ yd} = 3 \textup{ yd} ^{2}$ .

Report an Error

View Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View Tutors

Meg, M.Ed.
Certified Tutor

The University of Tennessee, Bachelor of Science, Hospitality Administration and Management. Lincoln Memorial University, Mas...

View Tutors

Frank
Certified Tutor

Ursinus College, Bachelor of Science, Mathematics. Lehigh University, Master of Science, Mathematics.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Chicago, ISEE Tutors in Boston, Math Tutors in Seattle, Reading Tutors in Denver, Computer Science Tutors in Los Angeles, MCAT Tutors in Denver, Math Tutors in Boston, French Tutors in Chicago, SSAT Tutors in San Diego, Reading Tutors in Phoenix

Popular Courses & Classes

ISEE Courses & Classes in Seattle, GRE Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Seattle, ACT Courses & Classes in Atlanta, ACT Courses & Classes in Phoenix, GMAT Courses & Classes in San Diego, LSAT Courses & Classes in Washington DC, ACT Courses & Classes in Miami, GRE Courses & Classes in Miami, ISEE Courses & Classes in Los Angeles

Popular Test Prep

GRE Test Prep in Philadelphia, MCAT Test Prep in Houston, ACT Test Prep in Phoenix, LSAT Test Prep in Miami, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Miami, ISEE Test Prep in Denver, GMAT Test Prep in Boston, ISEE Test Prep in Los Angeles, GRE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Geometry

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #11 : Triangles

Example Question #161 : Geometry

Example Question #1 : How To Find The Area Of A Trapezoid

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #101 : Geometry

Example Question #51 : Geometry

Example Question #52 : Geometry

Example Question #53 : Geometry

Example Question #54 : Geometry

Example Question #53 : Geometry

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: