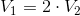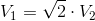Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Geometry

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #141 : Geometry

A circle has area $\frac{16 }{25}\pi$ . Give its circumference.

Possible Answers:

$\frac{4}{5} \pi$

$\frac{8}{5} \pi$

$\frac{256}{625} \pi$

$\frac{64}{625} \pi$

Correct answer:

$\frac{8}{5} \pi$

Explanation:

The area of a circle, given its radius , is

$A = \pi r^{2}$

Set $A = \frac{16 }{25}\pi$ to find the radius.

$\frac{16 }{25}\pi = \pi r^{2}$

$\frac{16 }{25}\pi \div \pi = \pi r^{2} \div \pi$

$\frac{16 }{25} = r^{2}$

$r = \sqrt{\frac{16}{25}} = \frac{\sqrt{16}}{\sqrt{25}} = \frac{4}{5}$

Multiply this radius by $2 \pi$ to find the circumference:

$\frac{4}{5} \cdot 2 \pi = \frac{8}{5} \pi$

Report an Error

Example Question #1325 : Concepts

Rectangle 2

The above rectangle has area 100. Give its perimeter in terms of .

Possible Answers:

$2N + \frac{200}{N}$

$100 N - N^{2}$

$50 N - N^{2}$

$N + \frac{100}{N}$

Correct answer:

$2N + \frac{200}{N}$

Explanation:

The width of a rectangle is the quotient of its area and its length, which are 100 and , respectively. Therefore, the width is $\frac{100}{N}$ . The four sides measure , , $\frac{100}{N}$ , and $\frac{100}{N}$ ; the perimeter is their sum, which is

$N + N + \frac{100}{N} + \frac{100}{N} = 2N + \frac{200}{N}$

Report an Error

Example Question #1326 : Concepts

Square a

The perimeter of the above square is 40% of what number?

Possible Answers:

57.6

120

19.2

360

Correct answer:

120

Explanation:

The perimeter of a square with sides of length 12 is 4 times this, or

$12 \times 4 = 48$ .

The number of which 48 is 40% can be found by dividing 48 by 40%, or $\frac{40}{100}$ :

$48 \div \frac{40}{100} = 48 \times \frac{100}{40}= 120$ ..

Report an Error

Example Question #1921 : Hspt Mathematics

What is the volume of a cube with a side of 9m?

Possible Answers:

27m^3

729m^3

9m^3

81m^3

Correct answer:

729m^3

Explanation:

Since volume is length times width times height, and every side on a cube is equal, multiply

$9\cdot 9\cdot 9=729$

The volume of this cube is 729 .

Report an Error

Example Question #1922 : Hspt Mathematics

A cube has six square faces, each with area 64 square inches. Using the conversion factor 1 inch = 2.5 centimeters, give the volume of this cube in cubic centimeters, rounding to the nearest whole number.

Possible Answers:

8,000 cubic centimeters

800 cubic centimeters

4,000 cubic centimeters

400 cubic centimeters

2,000 cubic centimeters

Correct answer:

8,000 cubic centimeters

Explanation:

The volume of a cube is the cube of its sidelength, which is also the sidelength of each square face. This sidelength is the square root of the area 64:

$\sqrt{64}=8$ inches.

Multiply this by 2.5 to get the sidelength in centimeters:

$\times 2.5$ = 20 centimeters.

The cube of this is

$20^{3}$ =8000 cubic centimeters

Report an Error

Example Question #1923 : Hspt Mathematics

A cube has a side length of 5 inches. Give the volume and surface area of the cube.

Possible Answers:

25 in^3 ,75 in^2

25 in^3 ,150 in^2

125 in^3 ,150 in^2

125 in^3 ,75 in^2

250in^3, 150 in^2

Correct answer:

125 in^3 ,150 in^2

Explanation:

A cube has all edges the same length. The volume of a cube is found by multiplying the length of any edge by itself twice. As a formula:

Volume=s^3 where is the length of any edge of the cube.

The Surface Area of a cube can be calculated as 6s^2 .

So we get:

Volume =s^3=5^3=125 in^3

Surface area $=6s^2=6\times 5^2=6\times 25=150 in^2$

Report an Error

Example Question #164 : Geometry

The height of a cylinder is 3 inches and the radius of the circular end of the cylinder is 3 inches. Give the volume and surface area of the cylinder.

Possible Answers:

V=84.82 in^3, A=113.10in^2

V=84.78 in^3, A=123.04in^2

V=74.78 in^3, A=113.10in^2

V=74.78 in^3, A=103.04in^2

V=84.78 in^3, A=103.04in^2

Correct answer:

V=84.82 in^3, A=113.10in^2

Explanation:

The volume of a cylinder is found by multiplying the area of one end of the cylinder (base) by its height or:

$Volume=\pi r^2h$

where is the radius of the circular end of the cylinder and is the height of the cylinder. So we can write:

$Volume=\pi r^2h=\pi \times 3^2\times 3=84.82in^3$

The surface area of the cylinder is given by:

$A=2\pi r^2+2\pi rh$

where is the surface area of the cylinder, is the radius of the cylinder and is the height of the cylinder. So we can write:

$A=2\pi r^2+2\pi rh$

$A=2\pi (3)^2+2\pi \times 3\times 3$

$A=18\pi+18\pi$

$A=36\pi$

A=113.10

Report an Error

Example Question #1924 : Hspt Mathematics

The end (base) of a cylinder has an area of $16\pi$ square inches. If the height of the cylinder is half of the radius of the base of the cylinder, give the volume of the cylinder.

Possible Answers:

$32\pi$

$8\pi$

$16\pi$

Correct answer:

$32\pi$

Explanation:

The area of the end (base) of a cylinder is $\pi r^2$ , so we can write:

$\pi r^2=16\pi\Rightarrow r^2=16\Rightarrow r=4\ inches$

The height of the cylinder is half of the radius of the base of the cylinder, that means:

$h=\frac{r}{2}=\frac{4}{2}=2\ inches$

The volume of a cylinder is found by multiplying the area of one end of the cylinder (base) by its height:

$Volume=Area\times h=16\pi\times 2=32\pi$

$Volume=\pi r^2h=\pi\times 4^2\times 2=32\pi$

Report an Error

Example Question #1925 : Hspt Mathematics

We have two right cylinders. The radius of the base Cylinder 1 is $\sqrt{3}$ times more than that of Cylinder 2, and the height of Cylinder 2 is 4 times more than the height of Cylinder 1. The volume of Cylinder 1 is what fraction of the volume of Cylinder 2?

Possible Answers:

$V_{1}=\frac{3}{2}V_{2}$

$V_{1}=\frac{2}{3}V_{2}$

$V_{1}=V_{2}$

$V_{1}=\frac{4}{3}V_{2}$

$V_{1}=\frac{3}{4}V_{2}$

Correct answer:

$V_{1}=\frac{3}{4}V_{2}$

Explanation:

The volume of a cylinder is:

$V=\pi r^2h$

where is the volume of the cylinder, is the radius of the circular end of the cylinder, and is the height of the cylinder.

So we can write:

$V_{1}=\pi (r_{1})^2h_{1}$

and

$V_{2}=\pi (r_{2})^2h_{2}$

Now we can summarize the given information:

$r_{1}=\sqrt{3}\cdot r_{2}$

$h_{2}=4\cdot h_{1}\Rightarrow h_{1}=\frac{h_{2}}{4}$

Now substitute them in the $V_{1}$ formula:

$V_{1}=\pi (\sqrt{3}r_{2})^2\times \frac{h_{2}}{4}\Rightarrow V_{1}=\frac{3}{4}\pi (r_{2})^2\times h_{2}\Rightarrow V_{1}=\frac{3}{4}V_{2}$

Report an Error

Example Question #1926 : Hspt Mathematics

Two right cylinders have the same height. The radius of the base of the first cylinder is two times more than that of the second cylinder. Compare the volume of the two cylinders.

Possible Answers:

$V_{1}=4\cdot V_{2}$

$V_{1}=V_{2}$

$V_{1}=\sqrt{2}\cdot V_{2}$

$V_{1}=2\cdot V_{2}$

$V_{1}=3\cdot V_{2}$

Correct answer:

$V_{1}=4\cdot V_{2}$

Explanation:

The volume of a cylinder is:

$V=\pi r^2h$

where is the radius of the circular end of the cylinder and is the height of the cylinder. So we can write:

$V_{1}=\pi (r_{1})^2h_{1}$

$V_{2}=\pi (r_{2})^2h_{2}$

We know that

$h_{1}=h_{2}$

and

$r_{1}=2r_{2}$ .

So we can write:

$V_{1}=\pi (r_{1})^2h_{1}=\pi (2r_{2})^2\cdot h_{2}=4\pi (r_{2})^2h_{2}\Rightarrow V_{1}=4V_{2}$

Report an Error

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Tutors

Joseph
Certified Tutor

Old Dominion University, Bachelor of Science, Electrical Engineering. Western Governors University, Masters in Education, Mat...

View Tutors

Mike Bahaa
Certified Tutor

Concordia University-Ann Arbor, Master of Arts Teaching, Mathematics Teacher Education.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Seattle, Computer Science Tutors in Atlanta, ISEE Tutors in Dallas Fort Worth, SSAT Tutors in Los Angeles, Computer Science Tutors in San Diego, ACT Tutors in Dallas Fort Worth, SAT Tutors in Seattle, Math Tutors in Houston, English Tutors in Miami, GMAT Tutors in Boston

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, ISEE Courses & Classes in Seattle, GRE Courses & Classes in Washington DC, GRE Courses & Classes in Seattle, SAT Courses & Classes in Miami, GRE Courses & Classes in San Diego, ISEE Courses & Classes in Philadelphia, ACT Courses & Classes in Denver, SAT Courses & Classes in Houston, GMAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

GMAT Test Prep in Philadelphia, SSAT Test Prep in New York City, GMAT Test Prep in Los Angeles, GRE Test Prep in Washington DC, ISEE Test Prep in Seattle, ISEE Test Prep in New York City, GMAT Test Prep in Denver, GMAT Test Prep in Phoenix, LSAT Test Prep in Miami, GRE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Geometry

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #141 : Geometry

Example Question #1325 : Concepts

Example Question #1326 : Concepts

Example Question #1921 : Hspt Mathematics

Example Question #1922 : Hspt Mathematics

Example Question #1923 : Hspt Mathematics

Example Question #164 : Geometry

Example Question #1924 : Hspt Mathematics

Example Question #1925 : Hspt Mathematics

Example Question #1926 : Hspt Mathematics

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: