HSPT Math : Geometry
Study concepts, example questions & explanations for HSPT Math
All HSPT Math Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of The Rectangle
A hectare is a unit of area equal to 10,000 square meters.
A 150-hectare plot of land is rectangular and is 1.2 kilometers in width. Give the perimeter of this land.
150 hectares is equal to 
The width of this land is 1.2 kilometers, or 
The perimeter of the land is
Example Question #2 : How To Find The Perimeter Of The Rectangle
The length of a rectangle is two times as long as the width. The width is equal to 
Example Question #3 : How To Find The Perimeter Of The Rectangle
How many meters of fence are needed to enclose a rectangular field that has a length of 1000 meters and a width of 100 meters?
The perimeter of a rectangle is simply the sum of the four sides:
Example Question #31 : Quadrilaterals
The perimeter of a rectangle with a length of 
We know that:
where:
So we can write:
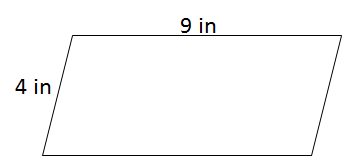
Example Question #1302 : Concepts
Find the perimeter of the parallelogram.
13 in
26 in
36 in
18 in
26 in
To find the perimeter of a parallelogram, add the lengths of the sides. Opposite sides of a parallelogram are equivalent.
Example Question #1303 : Concepts
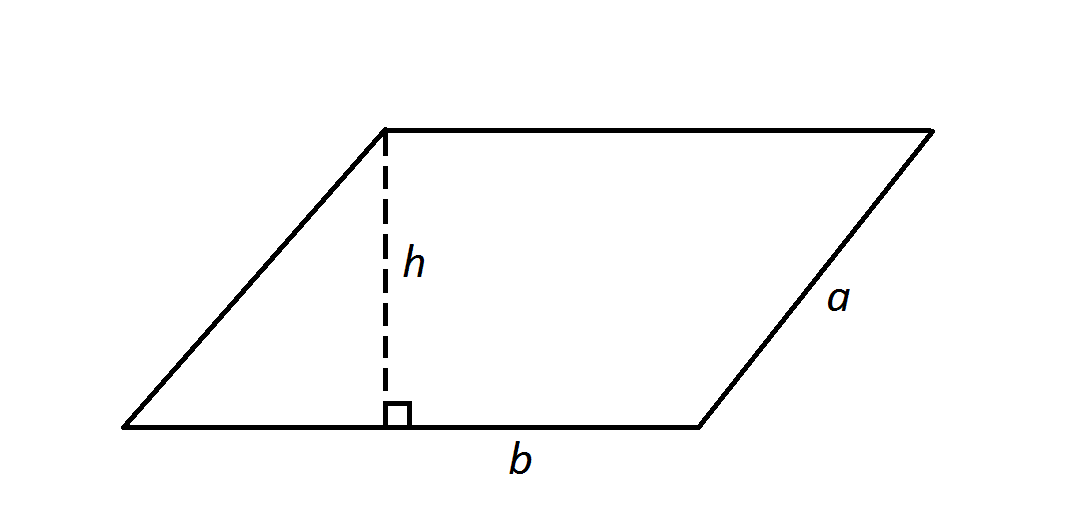
Note: Figure NOT drawn to scale.
Find the perimeter of the parallelogram in the diagram.
The perimeter of the parallelogram is the sum of the four side lengths - here, that formula becomes
Note that the height 
Example Question #4 : How To Find The Perimeter Of The Rectangle
What is the perimeter of a rectangle with a width of 3 and a length of 10?
13
12
26
30
60
26
The formula for the perimeter of a rectangle is 
Plug in our given values to solve:
Example Question #2 : Acute / Obtuse Triangles
Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?
30
0
15
The answer cannot be determined
10
10
The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.
Example Question #1 : Equilateral Triangles
A square rug border consists of a continuous pattern of equilateral triangles, with isosceles triangles as corners, one of which is shown above. If the length of each equilateral triangle side is 5 inches, and there are 40 triangles in total, what is the total perimeter of the rug?
The inner angles of the corner triangles is 30°.
188
200
180
124
208
188
There are 2 components to this problem. The first, and easier one, is recognizing how much of the perimeter the equilateral triangles take up—since there are 40 triangles in total, there must be 40 – 4 = 36 of these triangles. By observation, each contributes only 1 side to the overall perimeter, thus we can simply multiply 36(5) = 180" contribution.
The second component is the corner triangles—recognizing that the congruent sides are adjacent to the 5-inch equilateral triangles, and the congruent angles can be found by
180 = 30+2x → x = 75°
We can use ratios to find the unknown side:
75/5 = 30/y → 75y = 150 → y = 2''.
Since there are 4 corners to the square rug, 2(4) = 8'' contribution to the total perimeter. Adding the 2 components, we get 180+8 = 188 inch perimeter.
Example Question #121 : Geometry
A circle with a radius 2 in is inscribed in a square. What is the perimeter of the square?
28 in
16 in
12 in
32 in
24 in
16 in
To inscribe means to draw inside a figure so as to touch in as many places as possible without overlapping. The circle is inside the square such that the diameter of the circle is the same as the side of the square, so the side is actually 4 in. The perimeter of the square = 4s = 4 * 4 = 16 in.
All HSPT Math Resources
