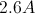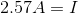For this problem, use Ohm's law: .

We are given the voltage and the resistance. Using these terms, we can solve for the current.

For this problem, use Ohm's law: .

We are given the current and the resistance. Using these terms, we can solve for the voltage.

Think of resistors as doors, preventing the flow of people (electrons). Imagine the following scenarios: a large group of people are in a room and all try to leave at once. If the five resistors are in series, that's like having all of these people trying to go through all five doors before they can leave. In a circuit, all the electrons in the current mast pass through every resistor.

If the resistors are in parallel, it's like having five separate doors from the room. All of a sudden, the group can leave MUCH faster, encountering less resistance to their flow out of the room. The path of the electrons can split, allowing each particle to pass through only one resistor.

From a formula perspective, the resistors in series are simply summed together to find the equivalent resistance.

 In parallel, however, the reciprocals are summed to find the reciprocal equivalent resistance.

Adding whole numbers will always give you a much greater result than adding fractions. For the exact same set of resistors, arrangement in series will have a greater total resistance than arrangement in parallel.

In basic resistors, energy lost due to resistance is converted into heat. In some cases, other conversions also take place (such as generation of light in a lightbulb), but heat is still dissipated along with any alternative conversations. Lightbulbs, batteries, and other types of resistors will become hot as current passes through them.

The formula for resistance is: 

Above,  is length,  is the cross-sectional area of the wire, and  is the resistivity of the material, and is a property of that material. The resistivity is constant for a given material, and thus cannot be changed by altering the dimensions of the wire.

For resistors aligned in series, the equivalent resistance is the sum of the individual resistances.

Since all the resistors in this problem are equal, we can simplify with multiplication.

For resistors in parallel, the equivalent resistance can be found by summing the reciprocals of the individual resistances, then taking the reciprocal of the resultant sum.

Since all the resistors in this problem are equal, we can simplify by multiplying.

The total resistance of resistors in series is the sum of the individual resistances.

In this case, we know the total resistance and the number of resistors, and we are told that all resistors are of equal strength. That means we can simplify this problem using multiplication.

We can use the total resistance to solve for the individual value.

When working in a series, the total resistance is the sum of the individual resistances.

Use the given values for each individual resistor to solve for the total resistance.

When working in a series, the total resistance is the sum of the individual resistances.

Use the given values for each individual resistor to solve for the total resistance.