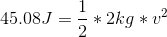The maximum velocity of the pendulum will be when the object has only kinetic energy. Using conservation of energy, we can set our initial potential energy to equal our "final" kinetic energy.

Plug in the given values and solve for the velocity.

The relationship between velocity and energy is:

We know the mass, but we need to find the total kinetic energy.

Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).

If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is .

Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.

The kinetic energy will also equal , due to conservation of energy.

Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.

Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.

The relationship between velocity and energy is:

We know the mass, but we need to find the total kinetic energy.

Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).

If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is .

Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.

The kinetic energy will also equal , due to conservation of energy.

Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.

Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.

For this problem, we need to use the law of conservation of energy. Since we are only looking at gravitational energy here and the orange starts at rest, we can say that the initial potential energy is equal to the final kinetic energy.

.

From here, we can expand the equation, using the formulas for gravitational potential energy and kinetic energy.

Notice that the mass cancels out form both sides.

For the height, make sure to keep that value negative as we are measuring the DISPLACEMENT rather than the distance travelled. Since displacement is a vector (magnitude and direction) we need to be clear that it travels down .

At this point, we need to remember that the square root of a positive number can be either positive or negative. Our velocity is a vector, so we will need to make sure we pick the answer choice with the appropriate direction. Since the orange is traveling downward, we know our final velocity must be negative.

To solve for the kinetic energy, we will need to use the equation:

Before we can plug in our given values, we must convert the mass from grams to kilograms. Remember, the SI unit for mass is kilograms, so most calculations will require this conversion.

Now we can use this mass and the given velocity to solve for the kinetic energy.

The relationship between velocity and energy is:

We know the mass, but we need to find the total kinetic energy.

Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).

If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is .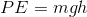

Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.

The kinetic energy will also equal , due to conservation of energy.

Using this value and our given mass, we can calculate the velocity from our original kinetic energy equation.

Since we are taking the square root, our answer can be either negative or positive. The final velocity of the book will be in the downward direction; thus, our final velocity should be negative.

Use Newton's laws to find the acceleration of the ball. Find the final speed of the ball, and then solve for kinetic energy.

Acceleration:

Final speed:

Kinetic energy:

The formula for kinetic energy is .

We first need to find the initial velocity in the vertical direction. To find the vertical velocity we use the equation .

We can plug in the given values for the angle and initial velocity to solve.

We know that the rock is going to travel a net distance of , as that is the distance between where the rock's initial and final positions. We now know the displacement, initial velocity, and acceleration, which will allow us to solve for the final velocity.

Now we have the mass and final velocity, allowing us to solve for the final kinetic energy.

At the top of the hill the skier has purely potential energy. At the bottom, she has purely kinetic energy. 

We can solve by understanding the conservation of energy. The skier's energy at the top of the hill will be equal to her energy at the bottom of the hill.

Using the equations for potential and kinetic energy, we can solve for the height of the hill.

The masses cancel, and we can plug in our final velocity and gravitational acceleration.

This formula solves for the change in height. The negative sign implies she travelled in a downward direction. Because the question is asking how tall the hill is, we use an absolute value.

We can use conservation of energy to solve. The potential energy when the astronaut is holding the rock will be equal to the kinetic energy just before it strikes the surface.

Now, we need to solve for , the gravity on the new planet. The masses will cancel out.

Plug in the given values and solve.