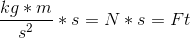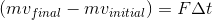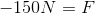Call Now to Set Up Tutoring:

(888) 888-0446

High School Physics : Calculating Momentum

Study concepts, example questions & explanations for High School Physics

Create An Account

All High School Physics Resources

6 Diagnostic Tests 233 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Calculating Momentum

A 2kg hammer moving with a velocity of $12\frac{m}{s}$ strikes a nail. The two are in contact for 0.2s , after which the hammer has a velocity of $0\frac{m}{s}$ . What is the force of the hammer on the nail?

Possible Answers:

-120N

130N

120N

-60N

60N

Correct answer:

120N

Explanation:

The fastest way to solve a problem like this is with momentum.

Remember that momentum is equal to mass times velocity: p=mv . We can rewrite this equation in terms of force.

$mv=(kg)(\frac{m}{s})=(kg)(\frac{m}{s})*(\frac{s}{s})$

$\frac{kg*m}{s^2}*s=N*s=Ft$

Using this transformation, we can see that momentum is also equal to force times time.

$\Delta p=F\Delta t$ can also be thought of as $(p_{final}-p_{initial})=F\Delta t$ .

Expand this equation to include our given values.

$(mv_{final}-mv_{initial})=F\Delta t$

Since the hammer is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.

$(2kg*0\frac{m}{s})-(2kg*12\frac{m}{s})=F*(0.2s)$

$(-2kg*12\frac{m}{s})=F*(0.2s)$

$(-24\frac{kg *m}{s})=F*(0.2s)$

$\frac{-24\frac{kg *m}{s}}{0.2s}=F$

-120N=F

This equation solves for the force of the nail on the hammer, as we were looking purely at the momentum of the hammer.

According to Newton's third law, $F_{hammer}=-F_{nail}$ . This means that if the nail exerts -120N of force on the hammer, then the hammer must exert 120N of force on the nail.

Report an Error

Example Question #52 : Momentum

A 1.8kg hammer moving with a velocity of $11\frac{m}{s}$ strikes a nail, after which the hammer has a velocity of $0\frac{m}{s}$ . If the hammer strikes the nail with 160N of force, how long were the two in contact?

Possible Answers:

0.12s

1.1s

0.06s

0.11s

0.33s

Correct answer:

0.12s

Explanation:

The fastest way to solve a problem like this is with momentum.

Remember that momentum is equal to mass times velocity: p=mv . We can rewrite this equation in terms of force.

$mv=(kg)(\frac{m}{s})=(kg)(\frac{m}{s})*(\frac{s}{s})$

$\frac{kg*m}{s^2}*s=N*s=Ft$

Using this transformation, we can see that momentum is also equal to force times time.

$\Delta p=F\Delta t$ can also be thought of as $(p_{final}-p_{initial})=F\Delta t$ .

Expand this equation to include our given values.

$(mv_{final}-mv_{initial})=F\Delta t$

Since the hammer is not moving at the end, its final velocity is zero. This allows us to set up the left side of our equation.

$(1.8kg*0\frac{m}{s})-(1.8kg*11\frac{m}{s})=F*\Delta t$

The problem gave us the force of the hammer on the nail, but not the force of the nail on the hammer, which is what we need for our equation since we are looking purely at the momentum of the hammer.

Fortunately, Newton's third law can help us. It states that $F_{hammer}=-F_{nail}$ . This means that if the hammer exerts 160N of force on the nail, then the nail must exert -160N of force on the hammer.

We can plug that value in for force and solve our equation for time.

$(0)-(1.8kg*11\frac{m}{s})=(-160N)(\Delta t)$

$(-1.8kg*11\frac{m}{s})=(-160N)(\Delta t)$

$-19.8\frac{kg*m}{s}=-160N*\Delta t$

$\frac{-19.8\frac{kg*m}{s}}{-160N}=\Delta t$

$0.12s=\Delta t$

Report an Error

Example Question #53 : Momentum

A 0.5kg ball hits a brick wall with a velocity of $10\frac{m}{s}$ and bounces back at the same speed. If the ball is in contact with the wall for 0.1s , what is the force exerted by the wall on the ball?

Possible Answers:

-20N

-5N

-100N

-10N

-200N

Correct answer:

-100N

Explanation:

The fastest way to solve a problem like this is with momentum.

Remember that momentum is equal to mass times velocity: p=mv . We can rewrite this equation in terms of force.

$mv=(kg)(\frac{m}{s})=(kg)(\frac{m}{s})*(\frac{s}{s})$

$\frac{kg*m}{s^2}*s=N*s=Ft$

Using this transformation, we can see that momentum is also equal to force times time.

$\Delta p=F\Delta t$ can also be thought of as $(p_{final}-p_{initial})=F\Delta t$ .

Expand this equation to include our given values.

$(mv_{final}-mv_{initial})=F\Delta t$

Even though the ball is bouncing back at the same "speed", its velocity will now be negative as it is moving in the opposite direction. Using these given values, we can solve for the force that acts on the ball.

$(0.5kg*-10\frac{m}{s})-(0.5kg*10\frac{m}{s})=F(0.1s)$

$(-5\frac{kg*m}{s})-(5\frac{kg*m}{s})=F(0.1s)$

$(-10\frac{kg*m}{s})=F(0.1s)$

$\frac{(-10\frac{kg*m}{s})}{0.1s}=F$

-100N=F

Our answer is negative because the force is moving the ball in the OPPOSITE direction from the way it was originally heading.

Report an Error

Example Question #31 : Calculating Momentum

A 13kg object moving at $2\frac{m}{s}$ strikes a 7kg object at rest. After the collision, the first object is motionless. What is the velocity of the second object?

Possible Answers:

$1.3\frac{m}{s}$

$0.27\frac{m}{s}$

$3.71\frac{m}{s}$

$1.1\frac{m}{s}$

$182\frac{m}{s}$

Correct answer:

$3.71\frac{m}{s}$

Explanation:

We need to solve this question be using conservation of momentum. (Note that the question can also be solved by using conservation of kinetic energy).

m_1v_1+m_2v_2=m_1v_3+m_2v_4

In this problem, the first object transfers all of its momentum to the second object. The initial velocity of the second object is zero, and the final velocity of the first object is zero. This means that:

m_1v_1=m_2v_2

Plug in the given values for the masses and initial velocity of the first mass to solve for the final velocity of the second mass.

m_1v_1=m_2v_2

$(13kg)(2\frac{m}{s})=(7kg)v_2$

$26\frac{kg*m}{s}=(7kg)v_2$

$\frac{26\frac{kg*m}{s}}{7kg}=v_2$

$3.7\frac{m}{s}=v_2$

Report an Error

Example Question #327 : Motion And Mechanics

A cat bats at a 0.08kg toy mouse. The mouse starts at rest and, after being struck, has a velocity of $12.1\frac{m}{s}$ . The cat's paw is in contact with the mouse for 0.22s . How much force did the cat exert on the mouse?

Possible Answers:

4.4N

0.23N

We need to know the acceleration of the mouse in order to solve

0.97N

0.21N

Correct answer:

4.4N

Explanation:

The fastest way to solve a problem like this is with momentum.

Remember that momentum is equal to mass times velocity: p=mv . We can rewrite this equation in terms of force.

$mv=(kg)(\frac{m}{s})=(kg)(\frac{m}{s})*(\frac{s}{s})$

$\frac{kg*m}{s^2}*s=N*s=Ft$

Using this transformation, we can see that momentum is also equal to force times time.

$\Delta p=F\Delta t$ can also be thought of as $(p_{final}-p_{initial})=F\Delta t$ .

Expand this equation to include our given values.

$(mv_{final}-mv_{initial})=F\Delta t$

Since the mouse starts at rest, the initial velocity must be zero. Using this information, the time of contact, the final velocity, and the given mass, we can solve for the force of the cat's paw on the mouse.

$(0.08kg)(12.1\frac{m}{s})-(0.08kg)(0\frac{m}{s})=F(0.22s)$

$0.968\frac{kg\cdot m}{s}-0\frac{kg\cdot m}{s}=F(0.22s)$

$0.968\ \frac{kg\cdot m}{s}=F(0.22s)$

$\frac{0.968\frac{kg\cdot m}{s}}{0.22s}=F$

4.4N=F

Report an Error

Example Question #32 : Calculating Momentum

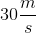
A 0.25kg ball hits a brick wall with a velocity of $30\frac{m}{s}$ and bounces back at the same speed. If the ball is in contact with the wall for 0.1s , what is the value of the force exerted by the wall on the ball?

Possible Answers:

100N

-150N

-100N

-300N

Correct answer:

-150N

Explanation:

The fastest way to solve a problem like this is with momentum.

Remember that momentum is equal to mass times velocity: 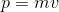p=mv . We can rewrite this equation in terms of force.

$mv=(kg)(\frac{m}{s})=(kg)(\frac{m}{s})*(\frac{s}{s})$

$\frac{kg*m}{s^2}*s=N*s=Ft$

Using this transformation, we can see that momentum is also equal to force times time.

$\Delta p=F\Delta t$ can also be thought of as $(p_{final}-p_{initial})=F\Delta t$ .

Expand this equation to include our given values.

$(mv_{final}-mv_{initial})=F\Delta t$

Even though the ball is bouncing back at the same "speed" its velocity will now be negative, as it is moving in the opposite direction. Using this understanding we can solve for the force in our equation.

$(0.25kg* -30\frac{m}{s})-(0.25kg* 30\frac{m}{s})=F(0.1s)$

$(-7.5\frac{kg\cdot m}{s})-(7.5\frac{kg\cdot m}{s})=F(0.1s)$

$(-15\frac{kg\cdot m}{s})=F(0.1s)$

$\frac{(-15\frac{kg\cdot m}{s})}{0.1s}=F$

-150N=F

Our answer is negative because the force is moving the ball in the OPPOSITE direction from the way it was originally heading.

Report an Error

View Tutors

Momodou
Certified Tutor

Rochester Institute of Technology, Bachelor in Arts, Animation and Special Effects.

View Tutors

Anthony
Certified Tutor

CUNY New York City College of Technology, Bachelor of Science, Civil Engineering.

View Tutors

Alejandro
Certified Tutor

Kennesaw State University, Bachelor of Science, Computer Software Engineering.

All High School Physics Resources

6 Diagnostic Tests 233 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Los Angeles, LSAT Tutors in San Francisco-Bay Area, ACT Tutors in Denver, Computer Science Tutors in Phoenix, ISEE Tutors in Boston, Reading Tutors in Dallas Fort Worth, English Tutors in Denver, Math Tutors in San Francisco-Bay Area, SAT Tutors in Philadelphia, ISEE Tutors in San Diego

Popular Courses & Classes

Spanish Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Denver, ISEE Courses & Classes in Seattle, ISEE Courses & Classes in Los Angeles, MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Washington DC, ACT Courses & Classes in Boston, SSAT Courses & Classes in Houston, GMAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Denver

Popular Test Prep

LSAT Test Prep in Los Angeles, ACT Test Prep in Boston, ACT Test Prep in Seattle, GMAT Test Prep in Seattle, SAT Test Prep in Boston, ACT Test Prep in Washington DC, LSAT Test Prep in Denver, GRE Test Prep in Philadelphia, GMAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Physics : Calculating Momentum

Study concepts, example questions & explanations for High School Physics

All High School Physics Resources

Example Questions

Example Question #31 : Calculating Momentum

Example Question #52 : Momentum

Example Question #53 : Momentum

Example Question #31 : Calculating Momentum

Example Question #327 : Motion And Mechanics

Example Question #32 : Calculating Momentum

All High School Physics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: