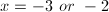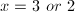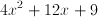All High School Math Resources
Example Questions
Example Question #1 : Quadratic Equations And Inequalities
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify.
Example Question #2 : Understanding Quadratic Equations
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
Example Question #1 : Quadratic Equations And Inequalities
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
Example Question #4 : Understanding Quadratic Equations
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
Example Question #1 : Understanding Quadratic Equations
FOIL 
Remember FOIL stands for First Outer Inner Last. That means we can take 

Simplify to get 
Example Question #6 : Understanding Quadratic Equations
FOIL 


Remember that FOIL stands for First Outer Inner Last.
For this problem, that would be 
Simplify that to 
Example Question #7 : Understanding Quadratic Equations
FOIL 
Remember that FOIL stands for First Outer Inner Last.
For this problem that would give us:
Simplify.
Example Question #8 : Understanding Quadratic Equations
FOIL 
Remember that FOIL stands for First Outer Inner Last.
For this problem that would give us:
Simplify:
Example Question #1 : Quadratic Equations And Inequalities
Solve the equation for 
Cross multiply.
Set the equation equal to zero.
Factor to find the roots of the polynomial.

Example Question #21 : Quadratic Equations And Inequalities
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify.
Certified Tutor
Certified Tutor
All High School Math Resources